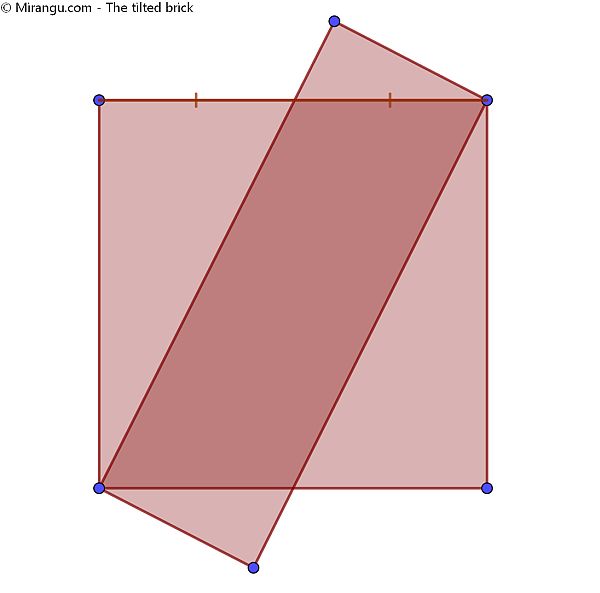
A rectangle is covering a square such that they share a diagonal and the top side of the square is divided in half as shown. What fraction of the square is covered by the rectangle? And what fraction of the rectangle is covered by the square?

Solution

Half of the square is covered by the rectangle, while 5/6 of the rectangle is covered by the square.

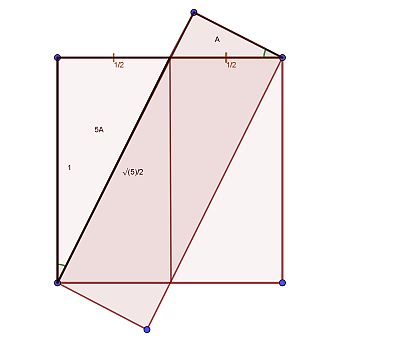
Draw a vertical line dividing the square in half. It is easily seen that the central shaded part is comprised of two quarter unit triangles adding up to half the square.

Finding out what part of the rectangle they make up is a bit more elaborate. Look at the little triangle sticking out on top of the square. By comparing its angles, it is readily seen to be similar to the quarter triangles mentioned earlier.

The question is: what is their proportion? Since the hypotenuse of the small triangle equals the short side of the large one, which, using the Pythagorean theorem, is √5 times smaller than it’s hypotenuse. Therefore, the small triangle has a 5 times smaller surface. It follows that the covered part is 5/6 of the whole rectangle.