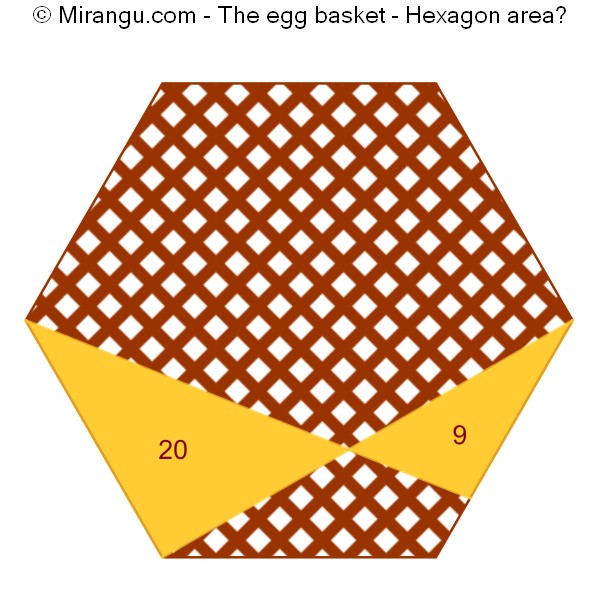
A regular hexagon with a diagonal and a line segment connecting a vertex to a point on the other side. The two triangle areas are given. What is the hexagon’s area?
Scroll down for a solution to this problem.
Solution
The hexagon area is 132.
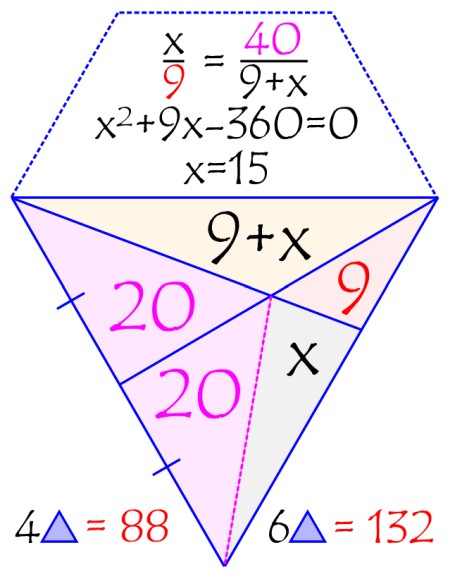
This clever solution by Crna extends half the regular hexagon by an extra equilateral triangle as shown, making another larger equilateral triangle. Divide the bottom quadrilateral in two triangles, one of which is equal to the 20-triangle.
The 9+x and the equation is derived from using the fact that triangles with equal height have areas proportional to their bases. Finally, the original hexagon area is 3/2 that of the equilateral triangle.
Poem
Ready for hunting Easter eggs
The basket in the hand
Looking around the house
The garden and the land
The eggs are hidden
Coloured, painted, nice
Chocolate eggs
For me and all my friends
A basket full so candy sweet
An Easter present, a secret place
A basket full of grace