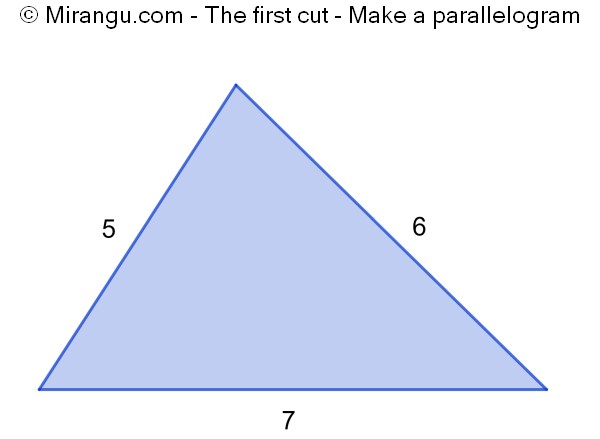
Using one straight cut, divide this triangle in two pieces. Paste them together to form a parallelogram with perimeter 19.
Scroll down for a solution to this problem.
Solution
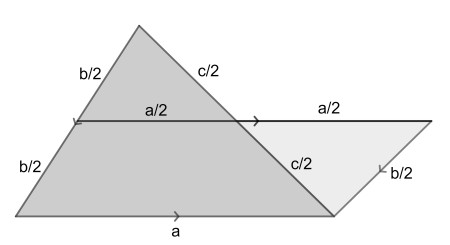
We consider the general case of a triangle with sides a, b and c. Cut parallel to side a through the midpoints of sides b and c. Then reflect the upper triangle in the c-midpoint as shown.
Since the horizontal parallel line segments have equal length, the connecting line segments are also parallel. Thus we have made a parallelogram with two sides of length a and two of length b/2. Its perimeter is 2a+b.
We could also have mirrored the upper triangle to the left. Also we could have cut parallel to b or c. So we have six possibilities having perimeters 2a+b, 2a+c, 2b+a, 2b+c, 2c+a and 2c+b. In case a=7, b=5 and c=6, we can see that both 2a+b and 2c+a equal 19. The first case is shown above.
Poem
The first cut
From a masterpiece
Can be a lot today
A painting or a writing
For a star’s shining
For a child’s loving
The love and inspiration
And even the protection
Also deep creation
And in my eyes
A sculpture
The first cut
A bright piece, a scintillation.