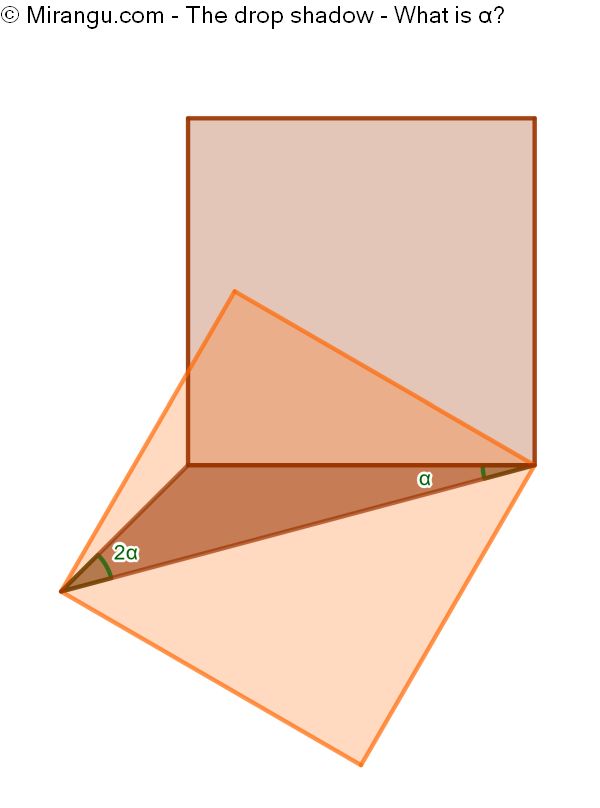
Two congruent squares share a vertex. What’s the angle α?

Solution

The angle α is 15°.

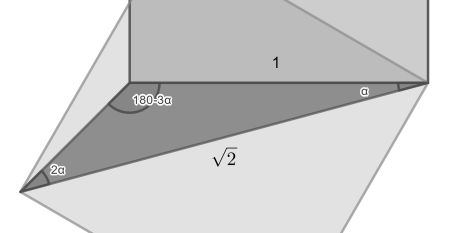
We are going to solve the puzzle by using trigonometry. Consider the shaded triangle. We can fill in the third angle and set the square side length to 1 for convenience. The diagonal then has length √2.

We can apply the Law of sines to get sin(180-3α)=sin(3α)=√2sin(2α). We use the triple- and double-angle equalities sin(3α)=3sin(α)-4sin³(α) and sin(2α)=2sin(α)cos(α) to get sin(α)[3-4sin²(α)-2√2cos(α)]=0.

We get from the diagram that α is larger than 0° and smaller than 45°. We can therefore discard the common sine-term. The other factor can be rewritten using sin²(α)+cos²(α)=1 as 4cos²(α)-2√2cos(α)-1=0.

This quadratic equation has two roots: cos(α)=√2(1±√3)/4, corresponding to α=15° and α=105°. The latter can be discarded.

Two congruent squares share a vertex. What’s the angle α? https://t.co/gVVlauwbwe pic.twitter.com/QspXZjIkbx

— Mirangu (@Mirangu1) January 11, 2021