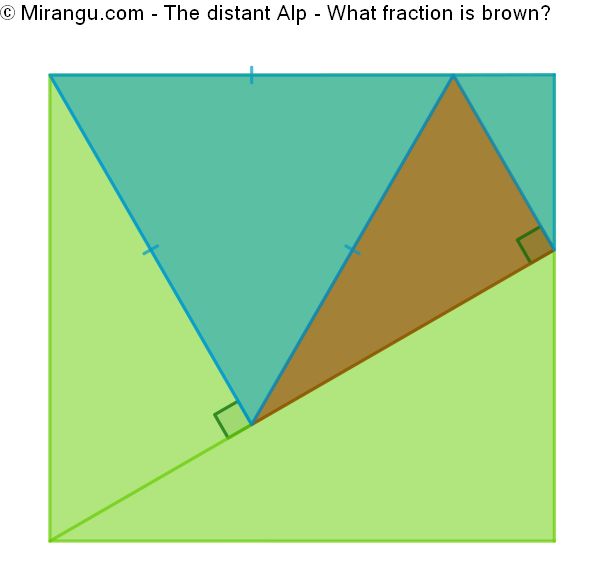
A rectangle containing five triangles. What fraction is brown?
Scroll down for a solution to this problem.
Solution
The brown fraction is 3/20.
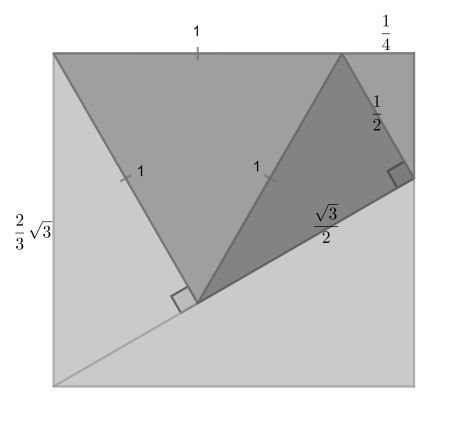
First we recognize an equilateral triangle surrounded by four 30-60-90 triangles. Of the latter it is well known that the sides have proportion 1 : √3 : 2. If one sets the equilateral side to 1, the other lengths can be deduced from this proportion as shown.
The brown triangle then has area √3/8. The rectangle is 5√3/6. The required fraction follows.
Visual solution
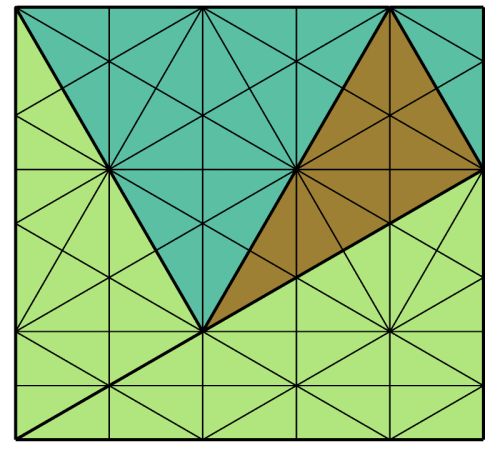
We were pleased to receive a completely visual solution from Uila, showing that the rectangle can be divided into 80 congruent triangles respecting all the triangle boundaries. Twelve of them are brown.
Poem
Our geometrical poet Belladonna composed the following lyrical poem:
Le fier glacier domine l’horizon
Les Alpes en dentelles, notre passion
Y fleurissent l’edelweiss et la valériane
Ainsi que la gentiane.
Silence ouaté, éternel
Sommets immaculés tournés vers le ciel
Métaphore étoilée brune et verte,
Ici représentée
Bella