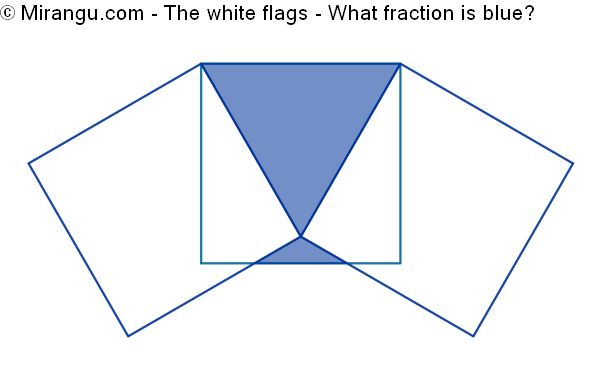
Three congruent squares and three shared vertices. What fraction is blue?
Scroll down for a solution to this problem.
Solution
The blue fraction is (2√3-3)/(2√3-1), which is approximately 0,19.
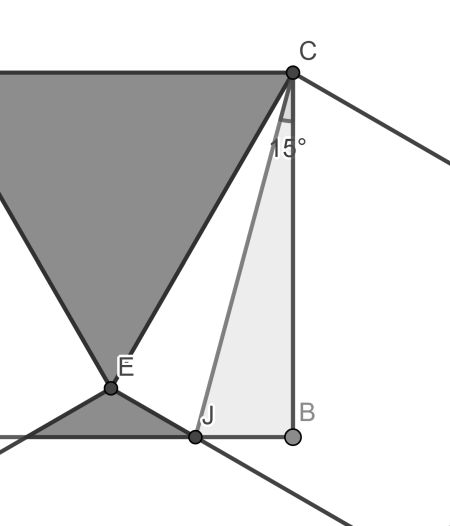
This solution hinges on finding the overlap regions. From reflection symmetry in the centre vertical they are congruent. Focussing on the right one, part EJC is congruent to BJC, due to reflection symmetry in CJ.
Now since the large blue triangle is equilateral, angle ECB is 30° and hence JCB is 15°. Setting the side of a square to 1, the area of right triangle BJC is readily found to be tan(15)/2, which is 1-√3/2.
Finally, we get for the blue area 1-2tan(15)=2√3-3, whereas the total area is 3-2tan(15)=2√3-1.
Poem
Our geometrical poet composed the following poem:
En symbole un drapeau
De notre pays le flambeau
Bleu, blanc rouge trois couleurs
Qui nous vont droit au coeur.
Drapeau qui partage nos joies, nos douleurs
En guerre comme en paix
Il est comme un phare ,
Notre lumière, il est toujours prêt.