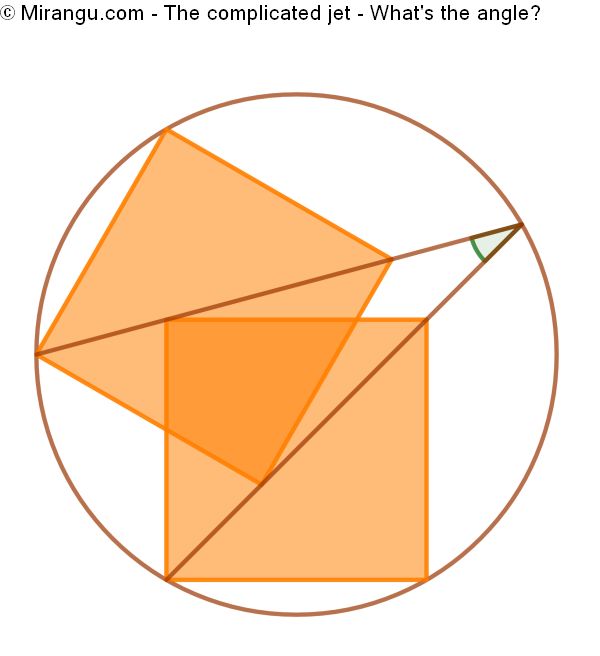
Two congruent squares inside a circle. The extended diagonals meet at the circle circumference. What’s their angle?

Solution

The angle is 30°.

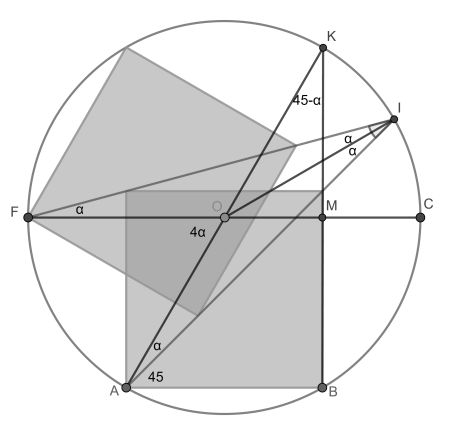
This proof was kindly provided by Ben Akkus. It folows these steps:

• Construct the circle centre O and draw the radius to point I. From reflection symmetry it bisects the requested angle in two angles α.
• Draw another radius to vertex A and from the isosceles triangle AOI deduce that angle OAI is α as well.
• Constructing the right triangle ABK and applying the converse of Thales, O must be the midpoint of AK. Angle AKB is found from the interior angle sum as 45-α.
• Then consider right triangle OMK. From the inscribed angle theorem, angle MOK is found to be 4α.
• Finally, again applying the interior angle sum, one gets 4α+90+45-α=180. This gives α=15°.

Solution 2

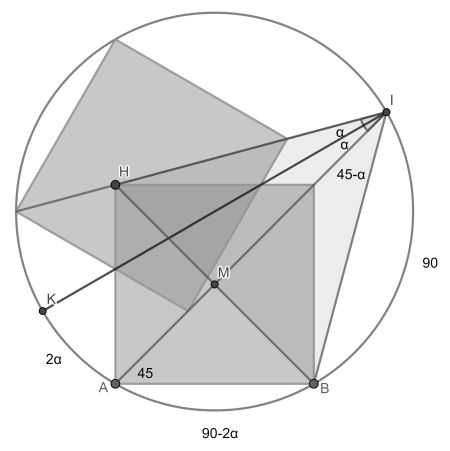
A solution that makes extensive use of the inscribed angle theorem is the one provided by Galip. It goes as follows.

• The diameter through I is drawn as well, again from reflection symmetry bisecting the requested angle in two angles α.
• Now the circular arc angles are evaluated of the semicircle from K to I. The 2α follows from the inscribed angle theorem. Equally, the 90 comes from looking at angle BAI. Therefore AB must be 90-2α.
• The triangle HIB is then considered. Since M is midpoint of base BH and MI is perpendicular to it, MI bisects angle HIB.
• Again applying the inscribed angle theorem, angle MIB must be 45-α and it is equal to MIH, which is 2α. This gives α=15°.

Visual solution

We were honoured to receive a unique and visual solution for The complicated jet from David Andriana:

Poem

Un JET dans son hangar
Un avion cher et rare
En France aviateurs d’élite
L’avion s’élance et se jette
C’est un avion vedette
C’est un jet de lumière
Pas utile pour la guerre
Seulement des voyageurs
D’1 bout à l’autre de la terre

Bella