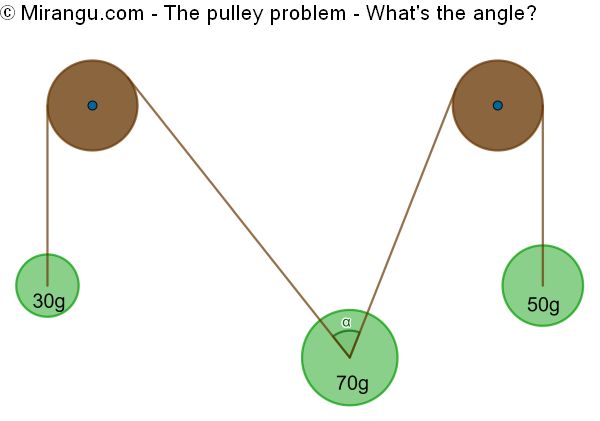
Two pulleys carrying three weights of 30, 70 and 50 grams. Given that the constellation is in equilibrium, what’s the angle?
Scroll down for a solution to this problem.
Solution
The angle is 60°.
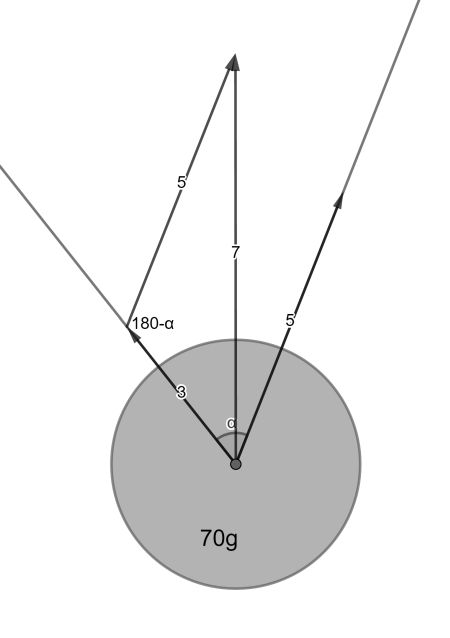
One needs to add up the force vectors working on the centre of gravity of the middle weight. The ones along the pulley ropes are scaled to 3 and 5 respectively. Since there is equilibrium, they exactly counterbalance the vertical vector from gravity which has size 7.
Now adding two vectors amounts to putting them head to tail as shown. They form a triangle, where one angle is 180-α, following from translational symmetry.
Since the sides are known, one can apply the cosine rule: 9+25-30cos(180-α)=49. This can be solved to give α=60°.
Please find here a tool for the general pulley problem. A video of the real thing can be found here.
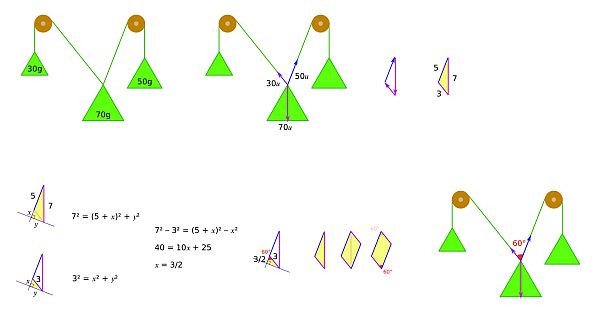
Visual solution
Poem
La poulie portent les poids
Jamais de charge ne ploient
Elle transmet le mouvement
Courroie de transmission
Et rapport de démultiplication
La poulie est altruiste
Sa vie n’est jamais triste
Elle soulève
Elle déplace
Elle démultiplie
Et sans cesse elle twiste.