Two regular hexagons share two vertices. What fraction of the area is purple?
Scroll down for a solution to this problem.
Solution
The purple fraction is 13/29.
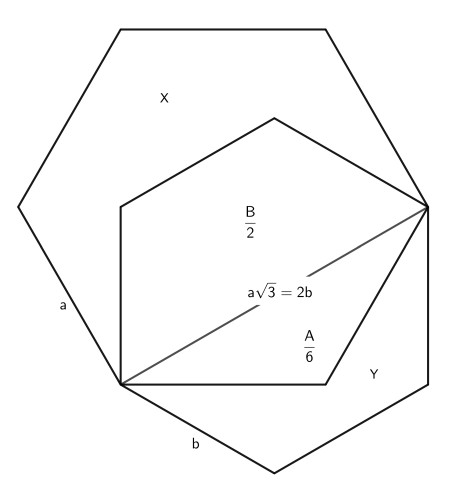
First, relate the diagonal connecting the shared vertices to the respective side lengths a and b. This gives b/a=√3/2 and therefore the smaller hexagon has area B that is 3/4 the area A of the larger one: B=3A/4.
Now splitting the purple area in two by this diagonal, it is easy two see that the two parts are A/6 and B/2. Thus, this overlap region is 13A/24 or equally 13B/18. We find that X=11A/24 and Y=5B/18=5A/24.
The required fraction is 13/(13+11+5)=13/29.
Poem
We can go in winter
Or also in summer
In boxcars travelling in coal dust and cinders
They sometimes are loaded with clothes or computers
Some men sold a boxcar filled with wheat flour
They made a good deal in less than 1 hour
They were so young and fun
They waved to the sun.

