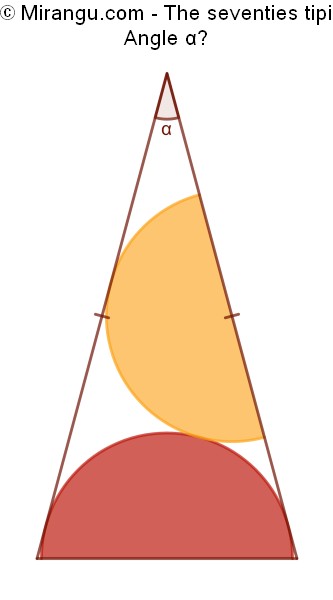
An isosceles triangle with two inscribed congruent semicircles. What is the angle α?

Solution

The angle α is 30°.

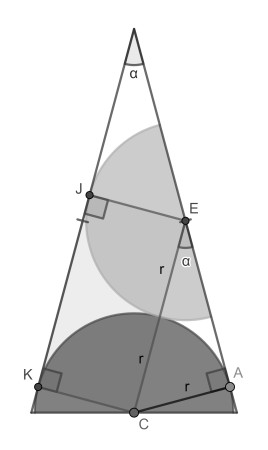
First draw the radii CK and EJ to the tangency points. Because of the two right angles and equal radii, EC must be parallel to JK and hence ∠CEA=α.

Now draw a radius CA to the third tangency point and notice that right triangle ACE has sides of r and 2r. We find that sin(α)=1/2 and hence α is 30°.

Notice that we didn’t use the fact that the triangle is isosceles, so strictly speaking the problem is over-constrained: the top angle would still be 30° in a non-isosceles triangle.