A square and an overlapping isosceles triangle. What is the angle α?
The glass piece
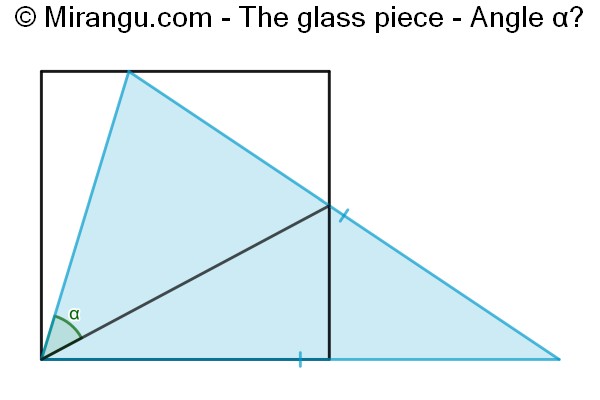

A square and an overlapping isosceles triangle. What is the angle α?
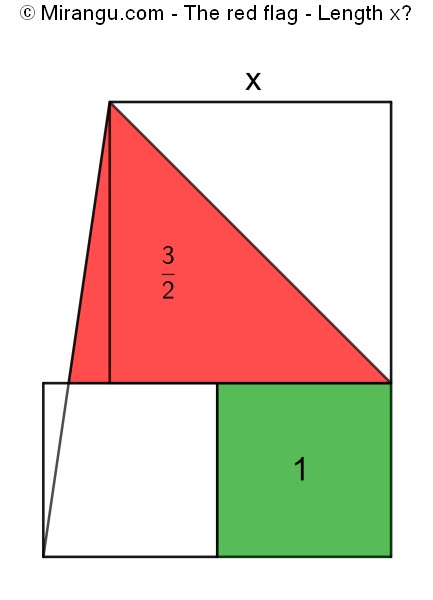
Three squares of which two vertices are connected. If the red triangle has area 1.5 and the green square area 1, what is the side length x?
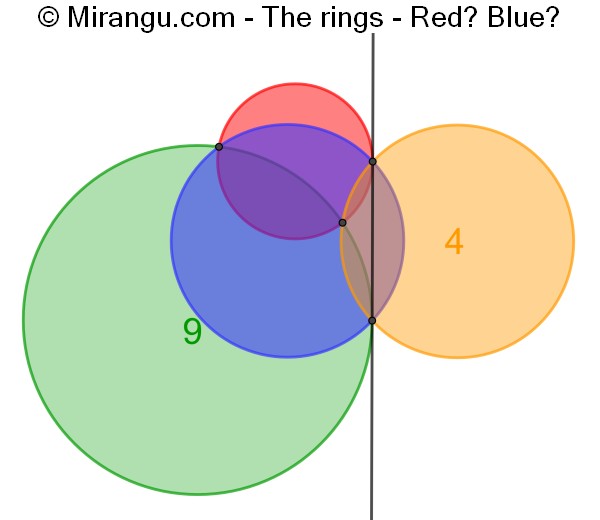
Four circles and a common tangent. The areas of the green and yellow circle are given. What are the areas of the red and blue circle?
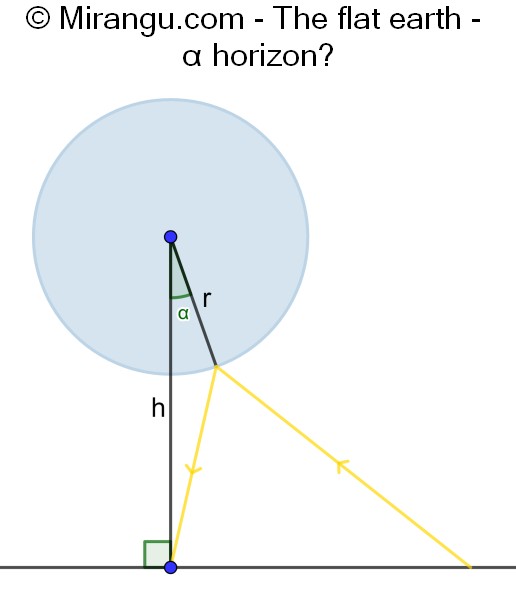
An observer is standing on a plane at h metres below the centre of a reflecting sphere of radius r. Another object on the plane is perceived at an angle α from the vertical. What is α of the horizon in terms of h and r?
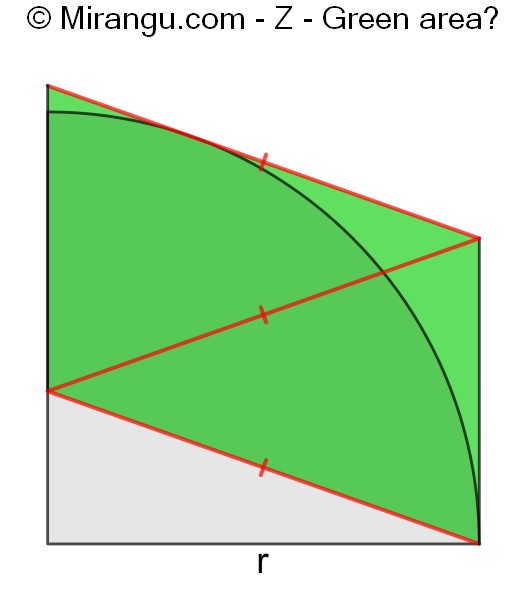
A green quadrilateral of which two sides are tangent to a quarter circle of radius r. What is its area?
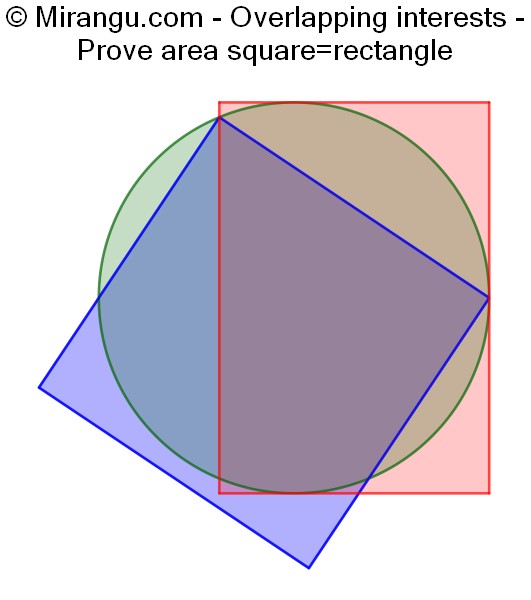
A square, a rectangle and a circle that partially overlap. One square vertex coincides with a rectangle-circle tangency point. Prove that the area of the square equals that of the rectangle.
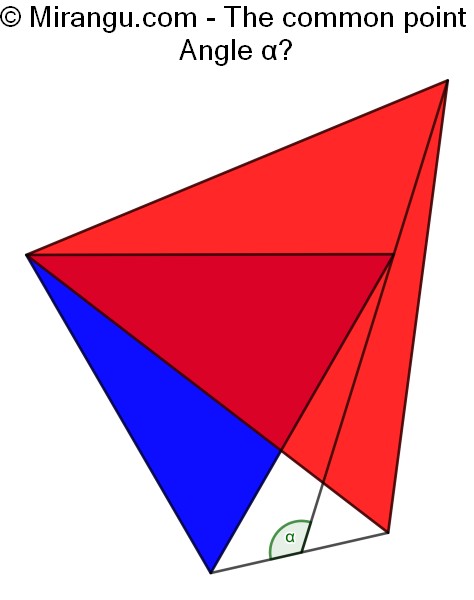
Two equilateral triangles share a vertex. What’s the angle α?
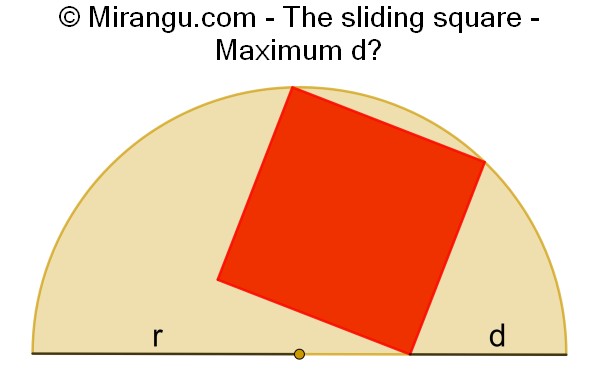
A square of variable size inscribed in a semicircle of radius r. What is the maximum distance d of the lowest square vertex to the nearest semicircle corner?
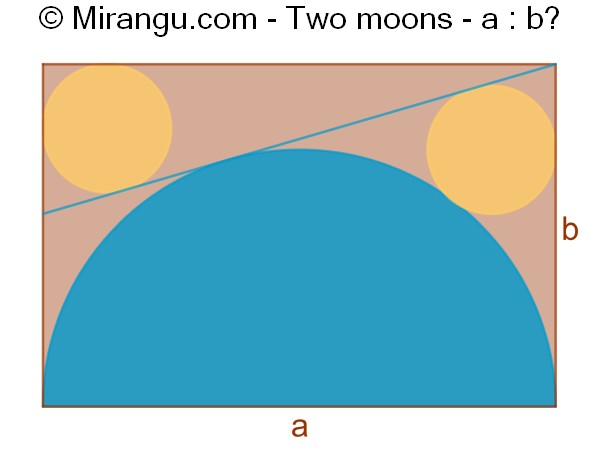
A rectangle with two congruent circles, a semicircle and a common tangent. What is the proportion of side lengths a : b?
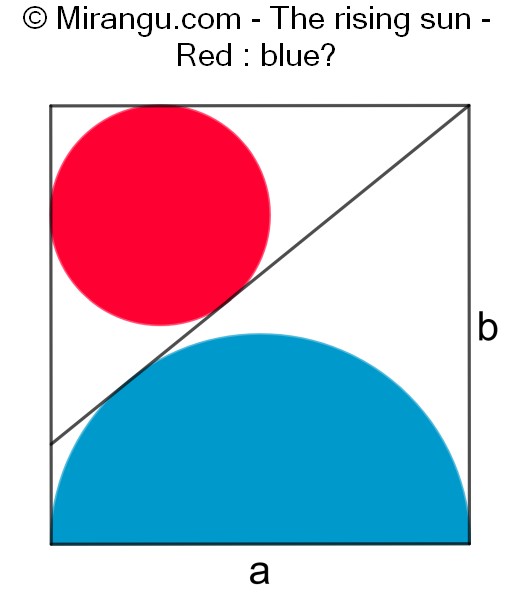
A rectangle with a circle and a semicircle. What is the proportion red : blue in terms of a and b?