A square of variable size inscribed in a semicircle of radius r. What is the maximum distance d of the lowest square vertex to the nearest semicircle corner?
Scroll down for a solution to this problem.
Solution
The maximum d is (2-√2)r.
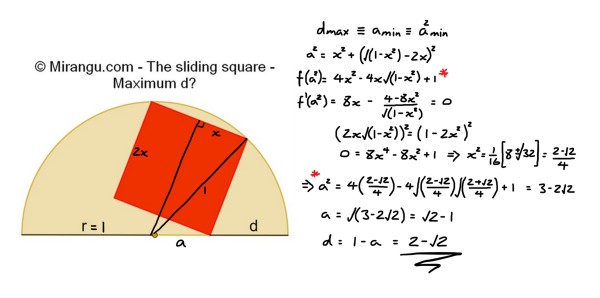
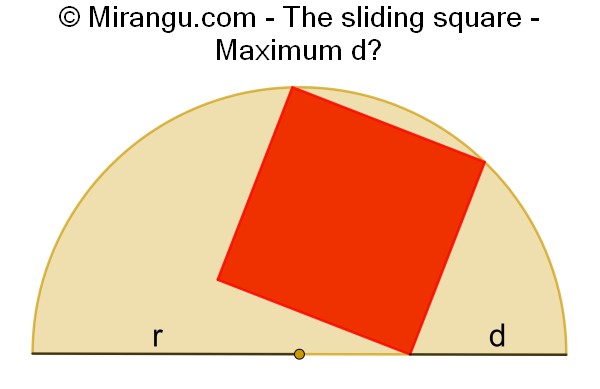
A square of variable size inscribed in a semicircle of radius r. What is the maximum distance d of the lowest square vertex to the nearest semicircle corner?
Scroll down for a solution to this problem.
The maximum d is (2-√2)r.

2 replies on “The sliding square”
I like your website.
The proof of “The sliding square” seems for me not complete:
The assumption that the angle at the midpoint of the circle opposite to the chord a is 2*theta ist not valid for every “sliding square”. So there is a gap in the proof.
Here are the corners of one of these sliding squares:
A(6-4*sqrt(6)|-8+4*sqrt(6))
B(14-4*sqrt(6)|0)
C(6|8)
D(-2|4*sqrt(6))
with C, D on the circle with center O(0|0) and radius 10.
Peter
Thank you Peter. You are right. I opted for another solution.