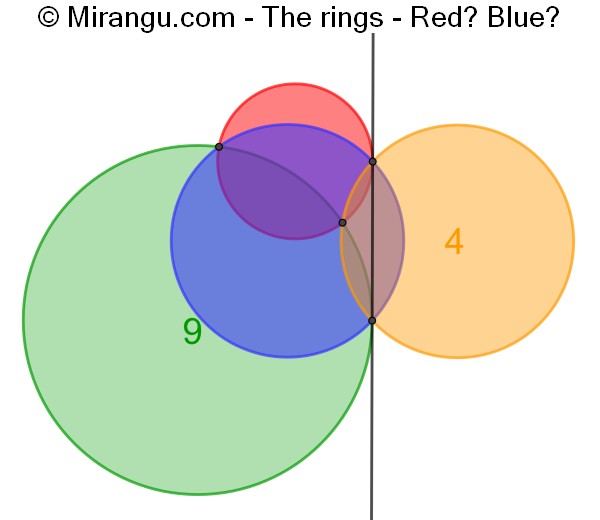
Four circles and a common tangent. The areas of the green and yellow circle are given. What are the areas of the red and blue circle?
Scroll down for a solution to this problem.
Solution
The red circle has area 16/9, blue is 4.
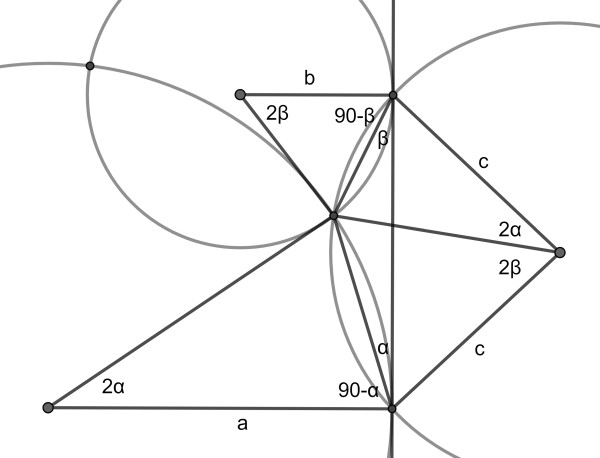
Let’s start with the red area. In the diagram above we draw several radii and connecting line segments. Using angles in isosceles triangles and the Inscribed angle theorem, we find the angles as shown.
Now it is easy to see we have two similar kites side by side. This gives a/c=c/b. Using green and yellow radii a and c it is straightforward to find the red radius b.
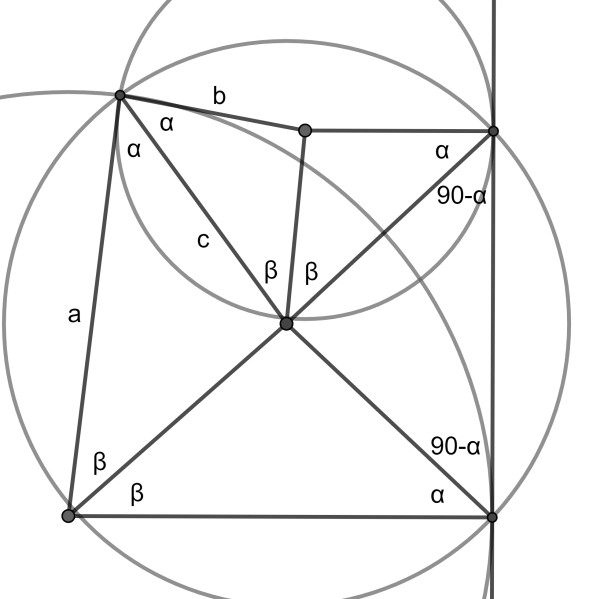
Now the blue area is found using the above diagram. Again using isosceles and similar triangles, we see emerging four similar triangles side by side. This also gives a/c=c/b and hence the blue area is equal to the yellow one.
Poem
99red balloons
Floating in the summer sky
Panic bells, it’s red alert
Theres something here from somewhere else
The war machine springs to life…
99 ministers meet…
Call the troops out in a hurry
This is it, boys, this is war
The president is on the line
(Nena, 99red bal)