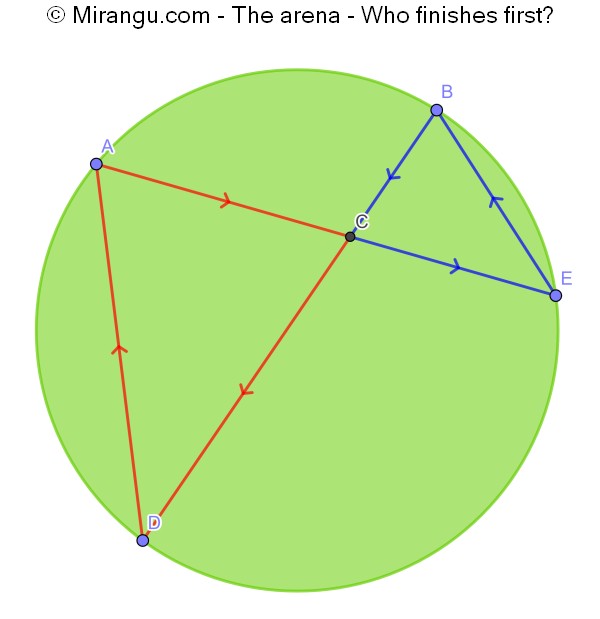
In a circular arena two contestants are leaving from points A and B. Their respective speeds are such that they would collide at point C, but just before they do they exchange directions. Then they hit the edge of the arena and return to their starting points. During the whole race, A and B move at constant but not necessarily equal speeds. Which contestant returns to his starting point first?
Scroll down for a solution to this problem.
Solution
The contestants return to start simultaniously.
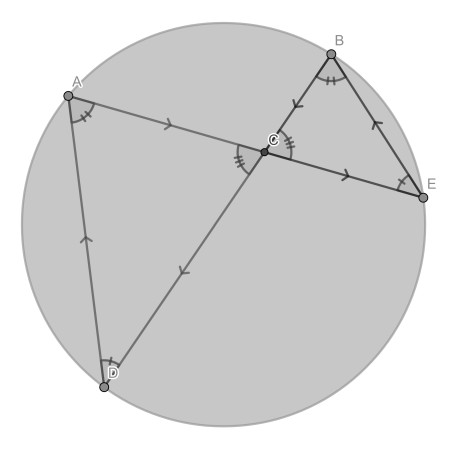
All angles are the same using the fact that same chords correspond to equal angles at the circle and opposing angles of two cutting lines are equal. Therefore triangles ACD and BCE are similar.
It is given that the speeds are such that the time to travel AC and BC respectively are the same. Since their speeds are constant and the length ratios of the sides are the same, this will also be true for the other two legs of the triangles. So they arrive at their starting points at the same time.
Poem
A bull lying on it’s side
Ready for fight
Ready for sacrifice
Jumping in the arena
The bull comes, goes, charges
The arena full of blood
The black eyed bull is wounded from fighting
The people in the arena watching
Without any
feeling
How the proud and strong bull is dying