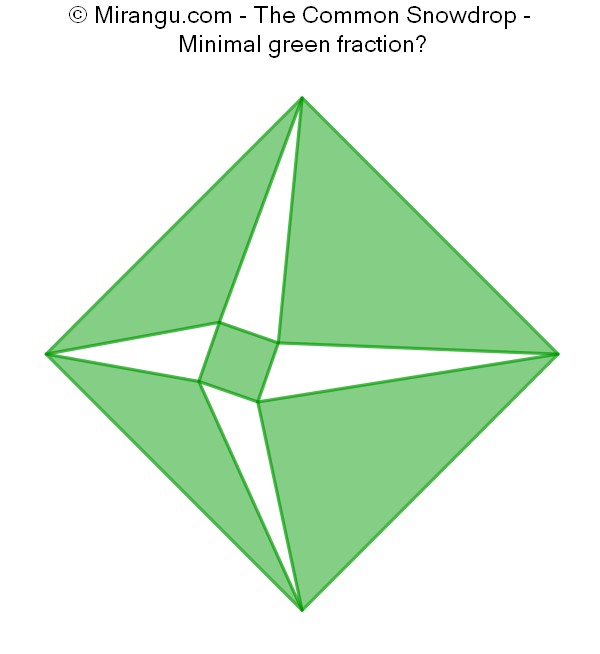
A square contains a smaller square. Their vertices are cyclically connected as shown, forming four triangles. What is the minimal green area fraction?
Scroll down for a solution to this problem.
Solution
The minimal green fraction is 1/2.
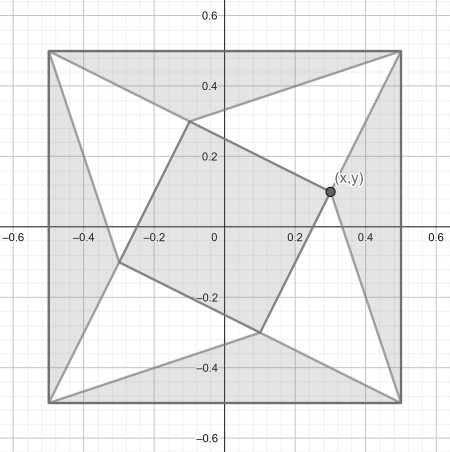
First it is seen that the problem satisfies translational symmetry of the small square centre, since the sum of the triangle heights is constant. We translate it such that the two squares are concentric and the figure has fourfold rotational symmetry.
We scale the large square to 1. Naming the vertex in the first quadrant (x,y), we can calculate the small square area as half the square of the diagonal, which evaluates to 2(x2+y2).
In the concentric case, all four triangles are congruent and have area (1/2-x)/2. Therefore the green area sums to A(x,y)=2(x2+y2+1/2-x). To find the extremes, we set dA/dx and dA/dy to 0. This gives x=1/2 and y=0. This is indeed a minimum and it evaluates to 1/2.
Find here a beautiful animation by Ignacio Larrosa Cañestro and notice how counterintuitive it looks as it approaches the minimum.
Poem
The snowdrop every year, still
Is growing and glooming with will
First greeting from the spring
It’s light pure and white shining
After a long sleep under snow
The little flower speaks to our hearts, it knows
Full of innocence
Opening humbly,
The snowdrop is an evidence