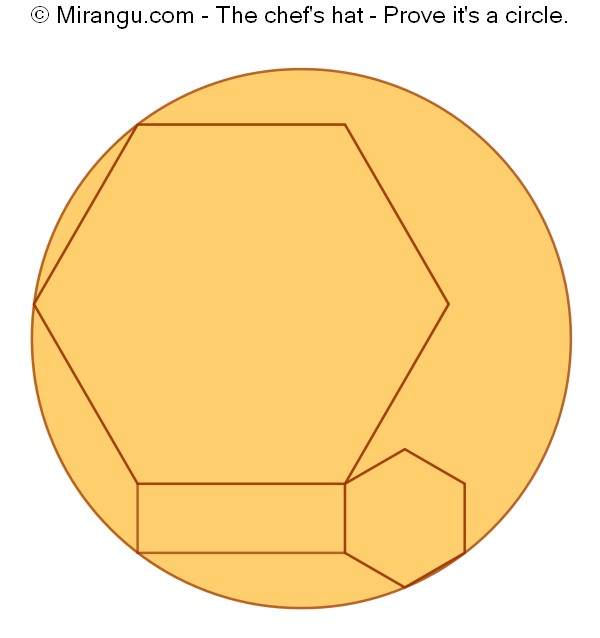
Two regular hexagons connected by a rectangle. Prove that the five vertices lie on a circle.
Scroll down for a solution to this problem.
Solution
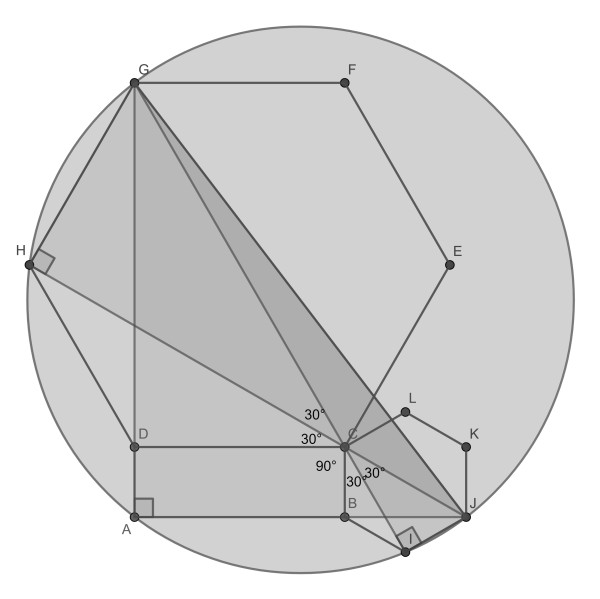
First draw the line segments GC. and CI. By adding the angles on the left side of these segments, we see they add up to 180. So GI is a straight line. Now triangle GIJ is a right triangle with hypothenuse GJ, and from the reversed Thales theorem it follows that I lies on the circle with GJ as diameter.
In a similar fashion triangles GHJ and GAJ are shown to be right triangles with hypothenuse GJ and so all points G, H, A, I and J lie on the same circle.