Two squares share a vertex. What’s the angle α?
Balancing act II
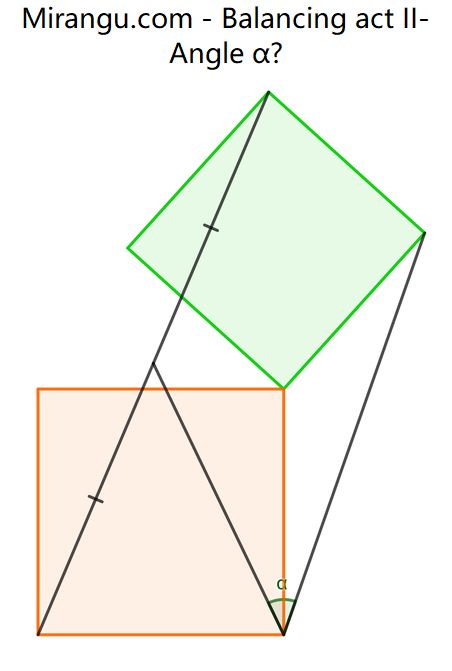

Two squares share a vertex. What’s the angle α?
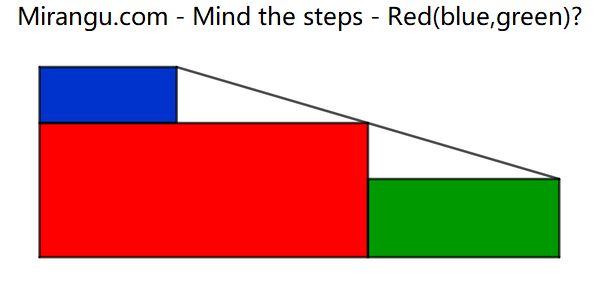
Three similar rectangles and a line segment. Express red in terms of blue and green.
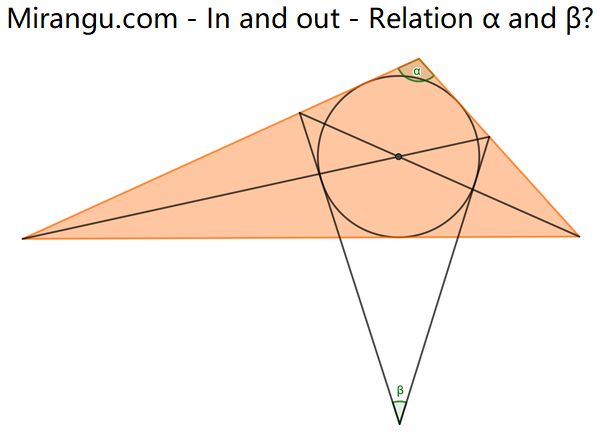
An obtuse triangle, of which α is the obtuse angle, with its incircle, two cevians and two tangents. Find a relation between α and β.
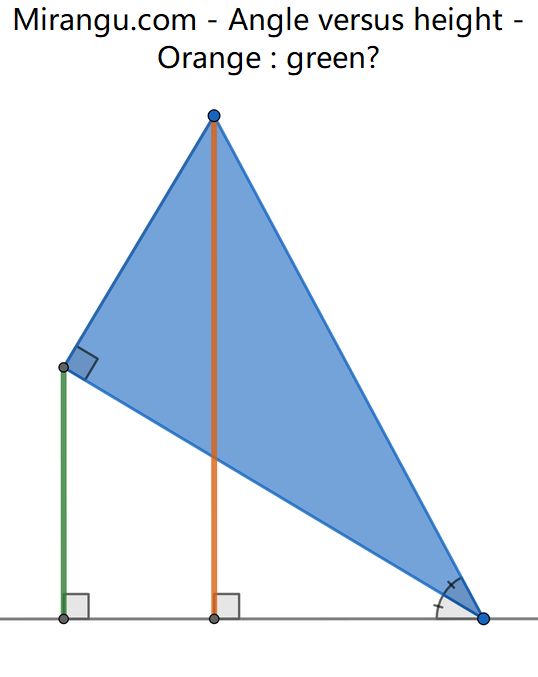
What is the ratio orange/green?
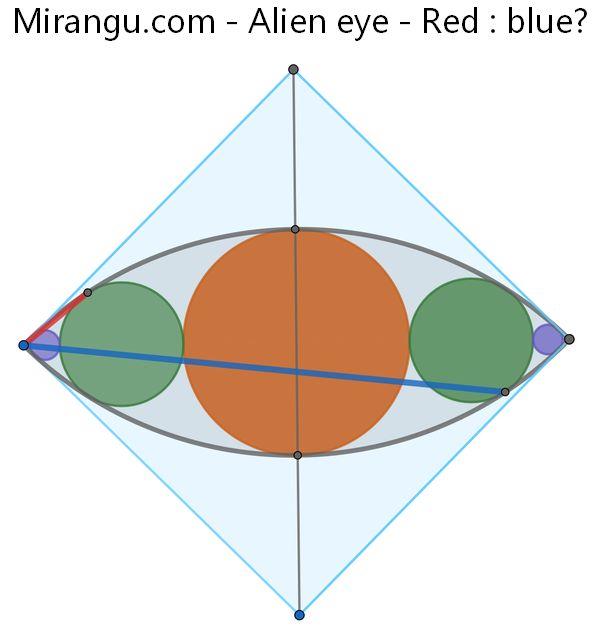
Two quarter-circles fit inside a square, and five circles fit inside the overlapped region, centred. What is the ratio of the (straight line) segment lengths red to blue? (The segments connect to points of tangency.)
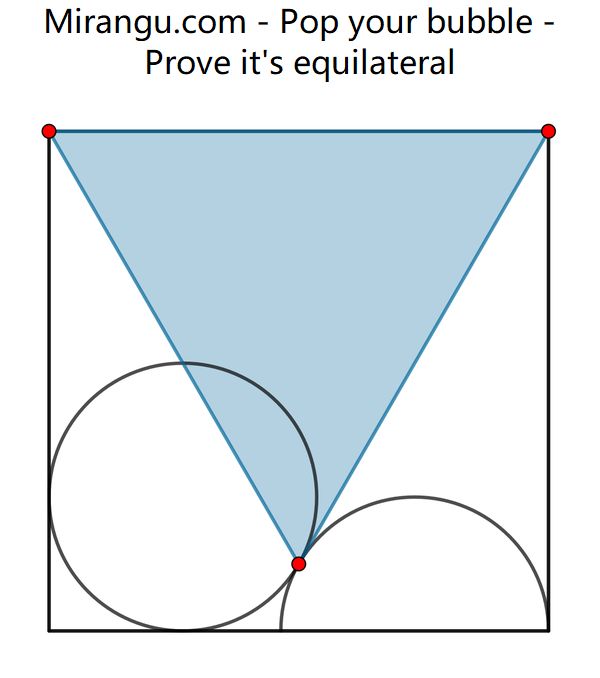
A square with a semicircle and a circle of equal radius. Their tangency point is shown. Prove that the red triangle is equilateral.
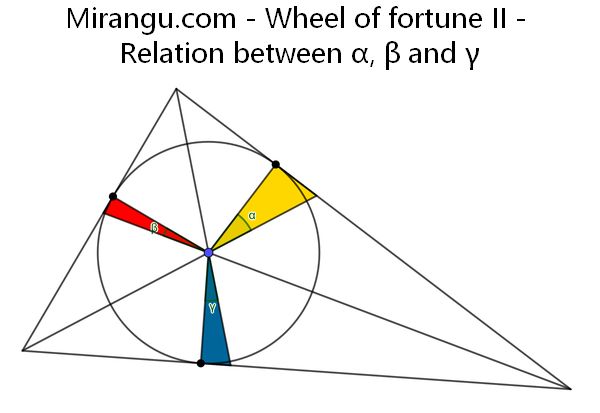
A triangle with its incircle and three cevians. The tangency points and incentre are shown. Find the relation between the angles α, β and γ.
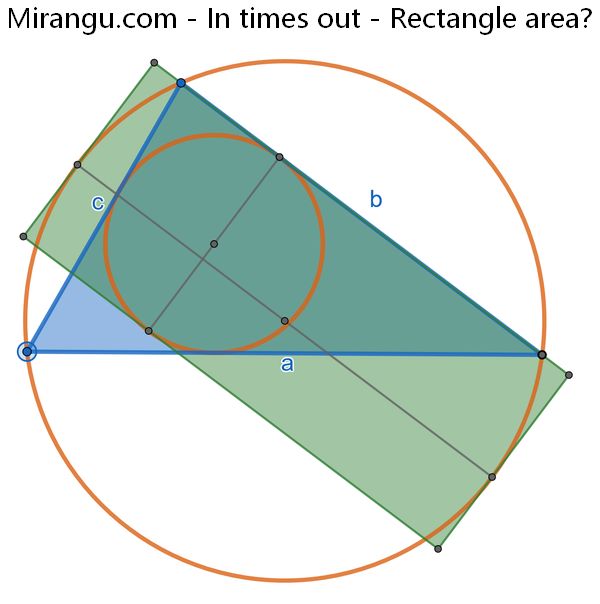
What is the area of the green rectangle, which has sides tangent to the incircle and circumcircle of a triangle with side lengths a, b, c.? (Write the answer as a multiple of a quotient of two elementary symmetric functions in a, b, c.)
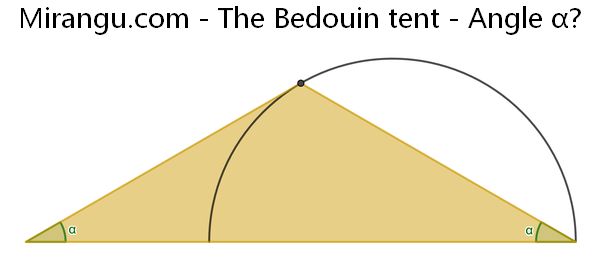
A semicircle and a triangle of which one side is tangent to the semicircle. What is the angle α?
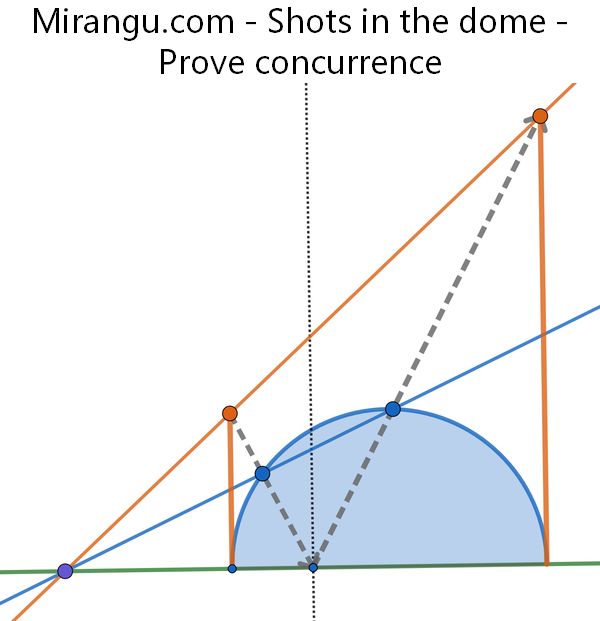
A beam from the top of one tower cuts through the dome, reflects off the ground, and hits the top of the other tower. Show that the line connecting the orange dots, the line connecting the blue dots, and the ground line are concurrent.
Improve your mental health with our new book “Vitamin G, 100 wholesome geometry puzzles”.
Order now