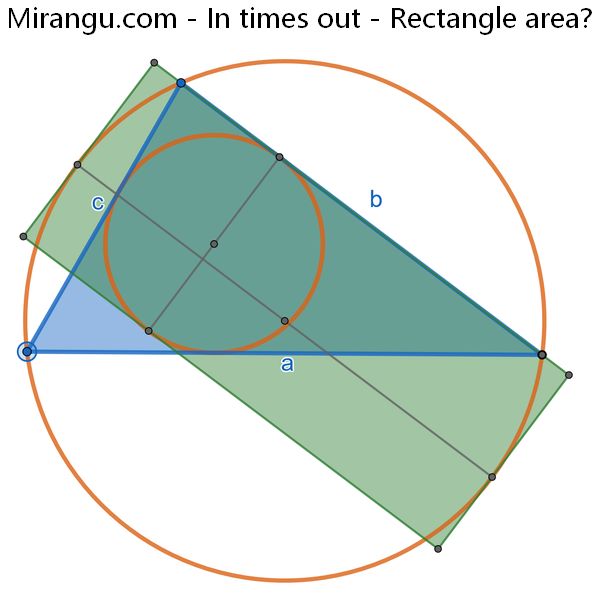
What is the area of the green rectangle, which has sides tangent to the incircle and circumcircle of a triangle with side lengths a, b, c.? (Write the answer as a multiple of a quotient of two elementary symmetric functions in a, b, c.)
Scroll down for a solution to this problem.
The rectangle area is 2abc/(a+b+c).
What is the area of the green rectangle, which has sides tangent to the incircle and circumcircle of a triangle with side lengths a, b, c.? (Write the answer as a multiple of a quotient of two elementary symmetric functions in a, b, c.) https://t.co/fj3fAEJVeQ By @MarshallWBuck pic.twitter.com/cYibu0RqXk
— Mirangu (@Mirangu1) February 20, 2024
2 replies on “In times out”
When I studied trigonometry as a child, I retained the law of sines only in the form a sin(B) = b sin(A). The extended results, involving the circumradius R and the triangle area A:
a/sin(A) = b/sin(B) = c/sin(C) = 2R, and R = abc/4A, or A = abc/4R ,
were either not in my textbook, or I forgot them instantly.
The purpose of this problem was to test that everyone out there is up to speed, unlike myself, on what is commonly called “the extended law of sines”.
See https://en.wikipedia.org/wiki/Law_of_sines for some history.
Also, the problem was set so that it was not necessary to use Heron’s formula for the area of triangle in terms of its sides, because the area A helpfully cancels out upon multiplying r = A/s by R = abc/4A, where s is the semiperimeter s= (a+b+c)/2.