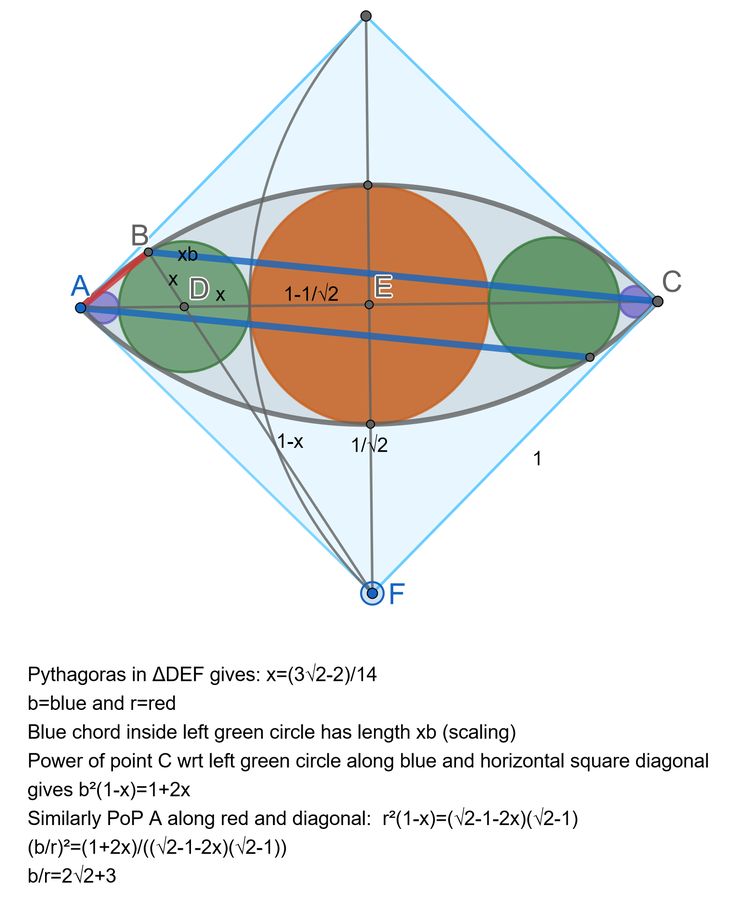
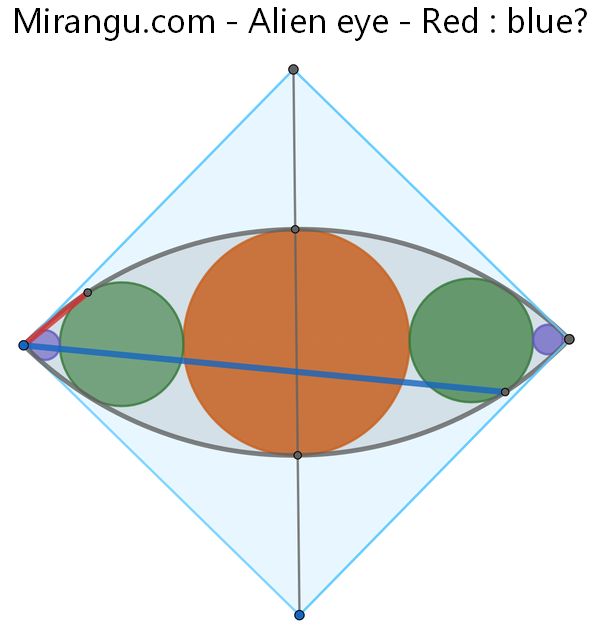
Two quarter-circles fit inside a square, and five circles fit inside the overlapped region, centred. What is the ratio of the (straight line) segment lengths red to blue? (The segments connect to points of tangency.)
Scroll down for a solution to this problem.
Solution
Blue : red is 2√2+3, which is approximately 5,83.
One reply on “Alien eye”
My solution started with the attached picture. The central orange circle in the eye becomes as large light-orange circle of the right, tangent to the two green lines at right angles to each other, which are the inversive images of the quarter circle boundaries of the eye. The other circles are also tangent to those lines, and tangent to the orange circle, so the radii are easily computed. The diagram leaves out the calculations, and leaves out the proof that the rightside orange circle has the same radius as the red circle of inversion on the left side. I post this here as “background” on how the problem was devised.