One corner of a rectangular piece of paper is folded as shown. Prove that the red line segments are concurrent.
Folding magic
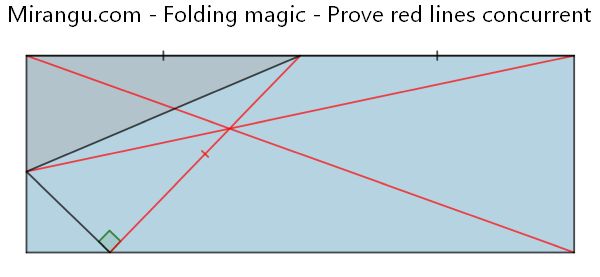

One corner of a rectangular piece of paper is folded as shown. Prove that the red line segments are concurrent.
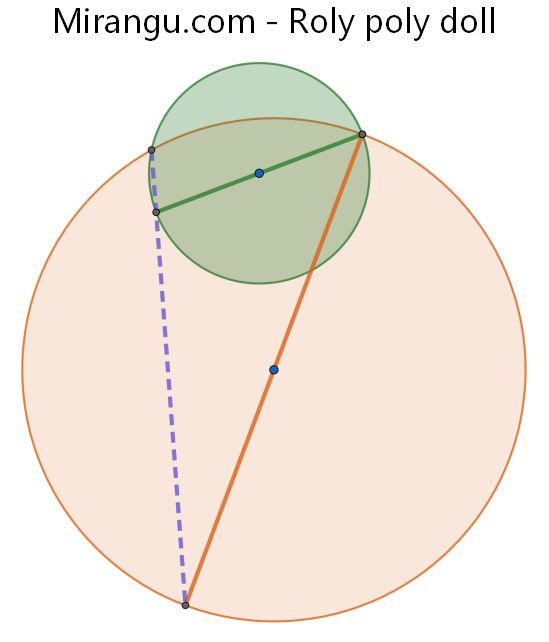
Two circles with diameters (green and orange) from one of the intersection points. Show that the other intersection point of the circles is on the (purple dotted) line connecting the other ends of the diameters.
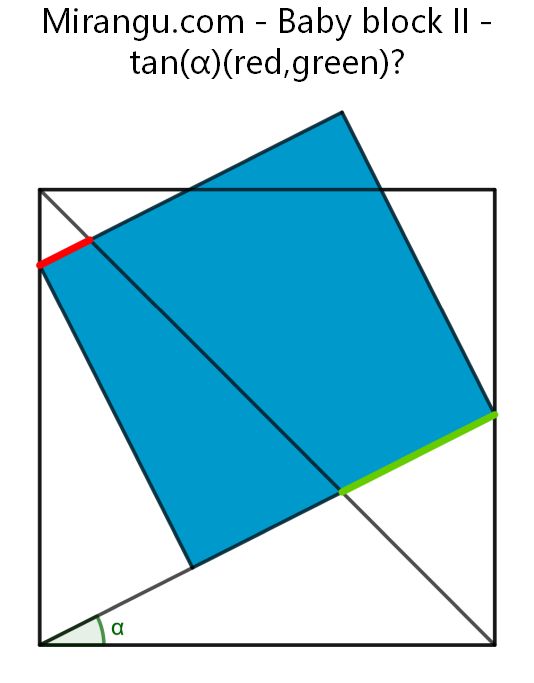
A square containing another square with an extended side. What is tan(α) in terms of the red and green segment lengths?
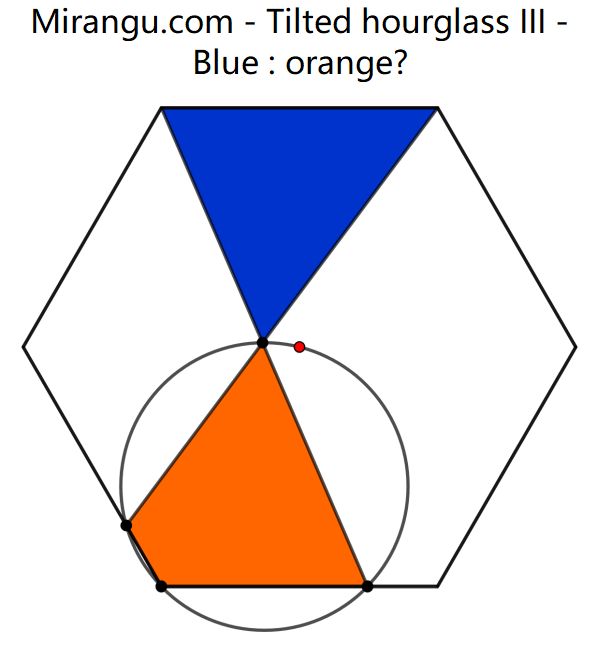
A regular hexagon, a circle through its red centre and two line segments. What’s blue : orange?
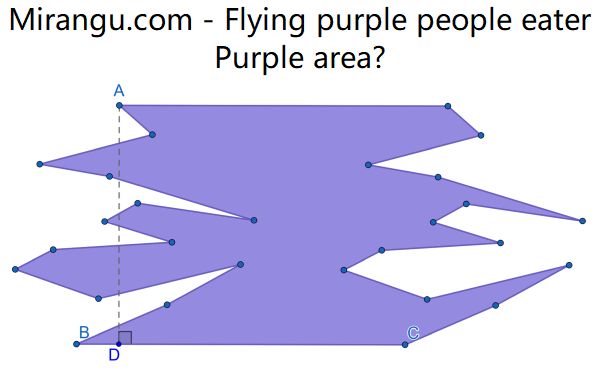
What is the area of the purple people eater, in terms of the lengths AD and BC?
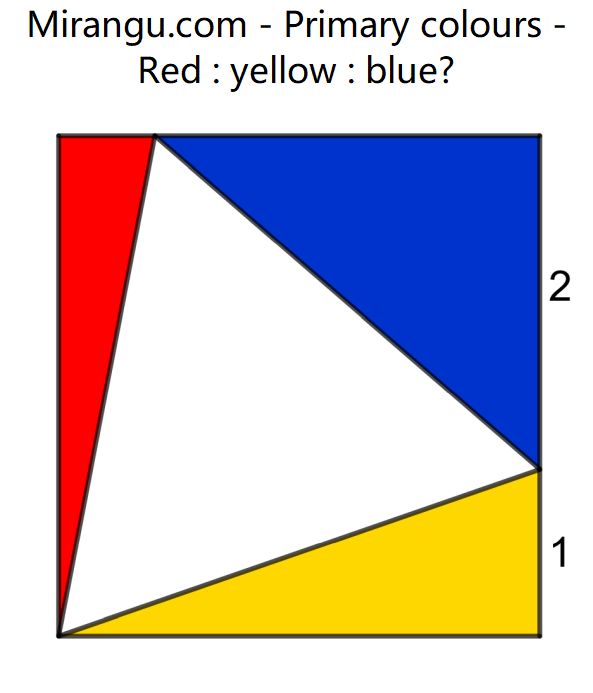
An equilateral triangle inside a rectangle. What is red : yellow : blue?
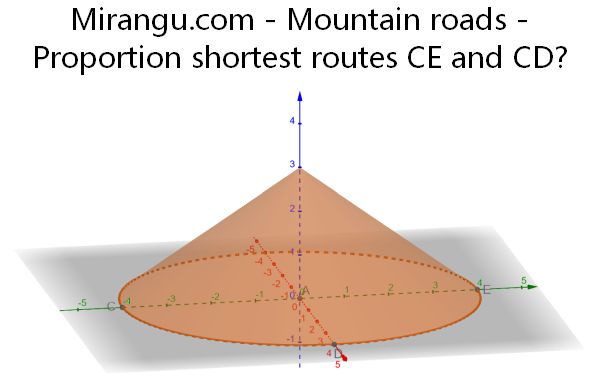
A circular mountain peak has coordinates (0,0,3) and its base has towns C=(-4,0,0), E=( 4,0,0) on opposite sides. Town D=(0,4,0) is halfway between them, around the base. A road goes partially up and down the mountain connecting C and E. Another road connects C and D. Both roads are shortest possible. What is the ratio of the road lengths?
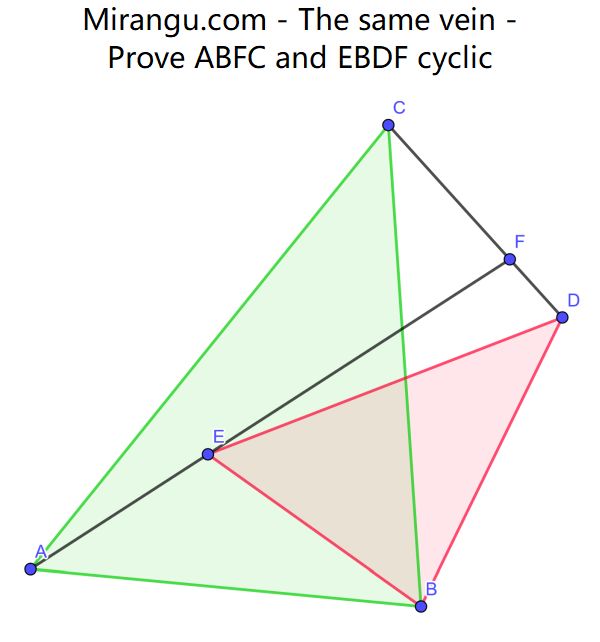
Two similar triangles ABC and EBD. Two line segments meet at point F. Prove that ABFC and EBDF are cyclic quadrilaterals.
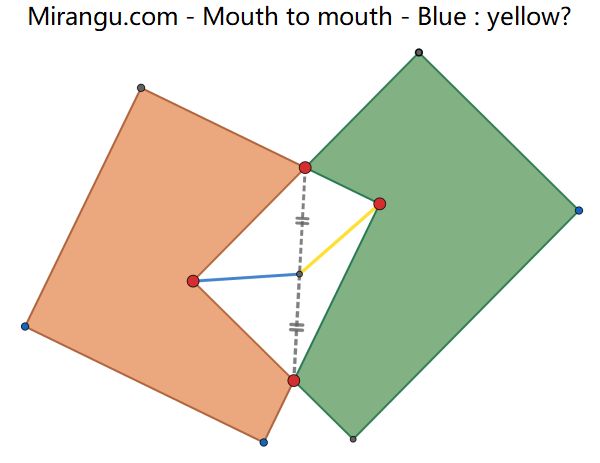
What is the ratio of the blue and yellow lines?
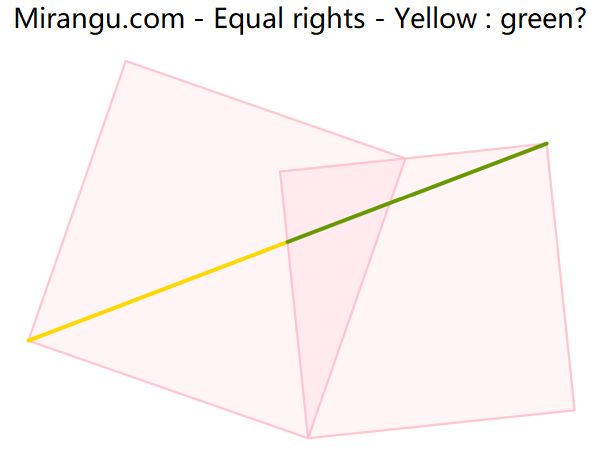
Two squares sharing a vertex. Two vertices are connected by a line segment. What is yellow : green?
Improve your mental health with our new book “Vitamin G, 100 wholesome geometry puzzles”.
Order now