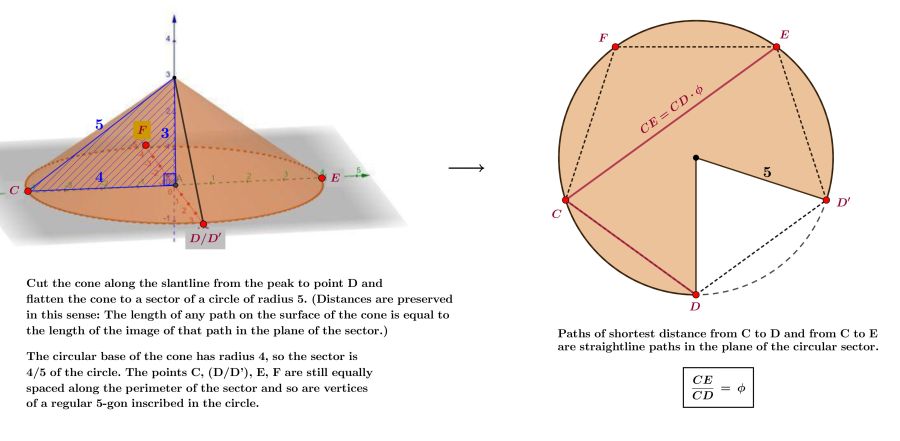
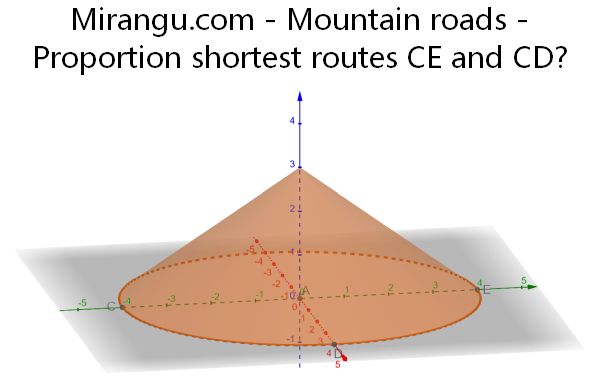
A circular mountain peak has coordinates (0,0,3) and its base has towns C=(-4,0,0), E=( 4,0,0) on opposite sides. Town D=(0,4,0) is halfway between them, around the base. A road goes partially up and down the mountain connecting C and E. Another road connects C and D. Both roads are shortest possible. What is the ratio of the road lengths?
Scroll down for a solution to this problem.
Solution
The proportion is φ.
3 replies on “Mountain roads”
Flatten the mountain to give a circle lacking a 72 degree slice.
Now consider straight lines in a plane rather than curves on a cone.
CE = 2x5cos(18)
CD=2x5sin(36)
So CD/CE = 2sin(18) =(sqr(5)-1)/2
It’s nice to see that someone was clever enough to check the website! The reason that Twitter feed doesn’t have it is that the text exceeded the Twitter maximum length.
Ratio ≈ 1.617