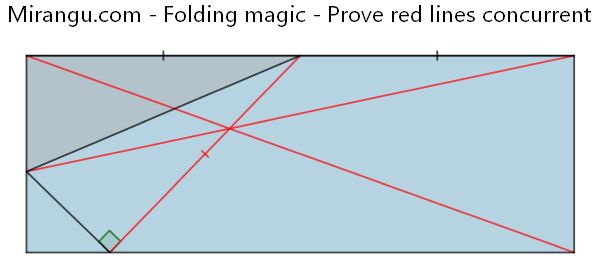
One corner of a rectangular piece of paper is folded as shown. Prove that the red line segments are concurrent.

Solution

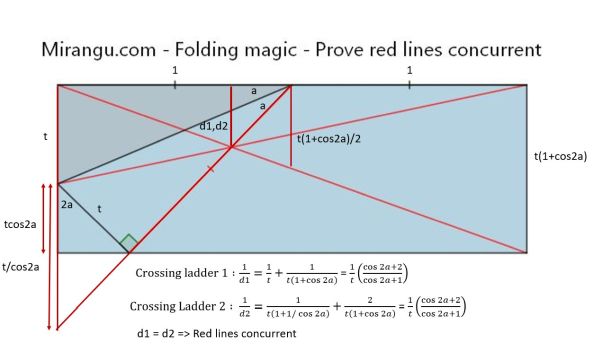
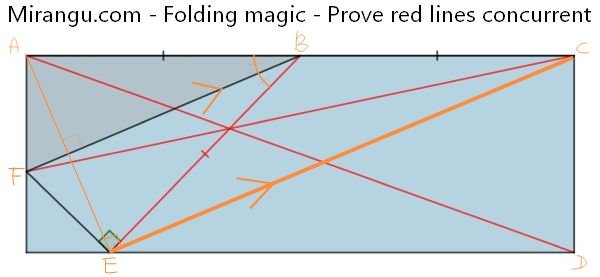
Let the intersection of AD and CF be G, ΔGAF∽ΔGDC, AG:GD=AF:CD (1) ∵
BF∥CE, ΔFAB∽ΔCDE, AF:CD=AB:DE (2)
Let the intersection of AD and BE be H, ΔHAB∽ΔHDE, AB:DE=AH:HD (3)
Due to (1)-(3), AG:GD=AH:HD, G and H are at the same point, ∴ red lines concurrent

One corner of a rectangular piece of paper is folded as shown. Prove that the red line segments are concurrent. https://t.co/w0TTBAYVCE Inspired by @faiz_sensei pic.twitter.com/QSbFQJljfY

— Mirangu (@Mirangu1) September 29, 2023