Four squares, three of which are coloured. What’s the area of the blue one?
The framing effect
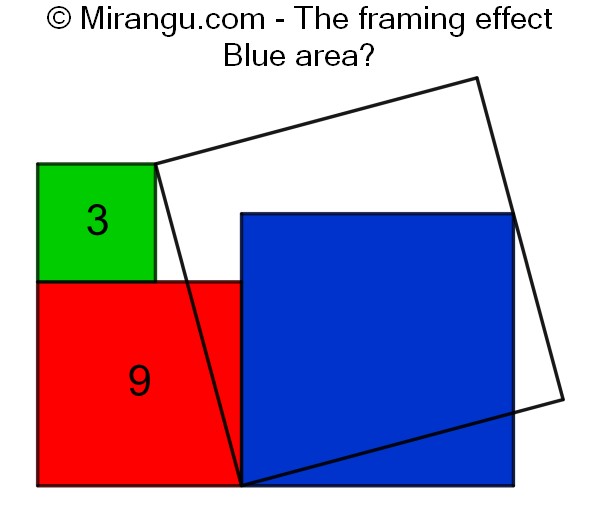

Four squares, three of which are coloured. What’s the area of the blue one?
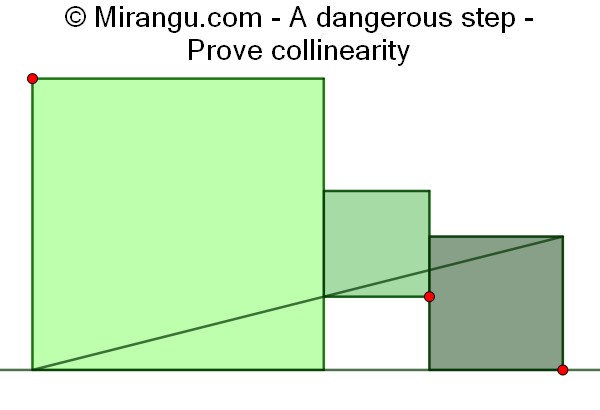
Three squares are placed in a row. Prove that the red vertices are collinear.
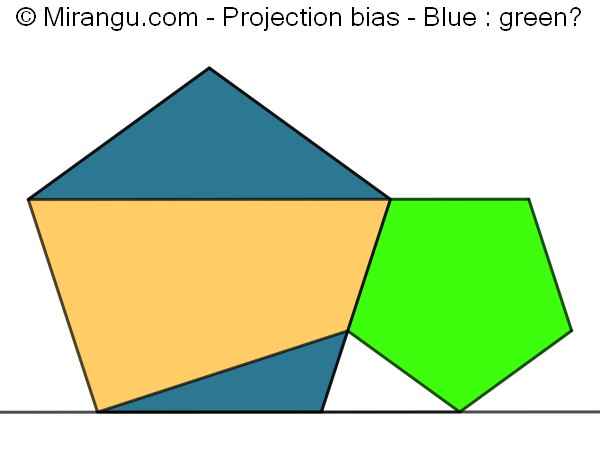
Two regular pentagons are placed side by side. What’s the proportion blue : green?
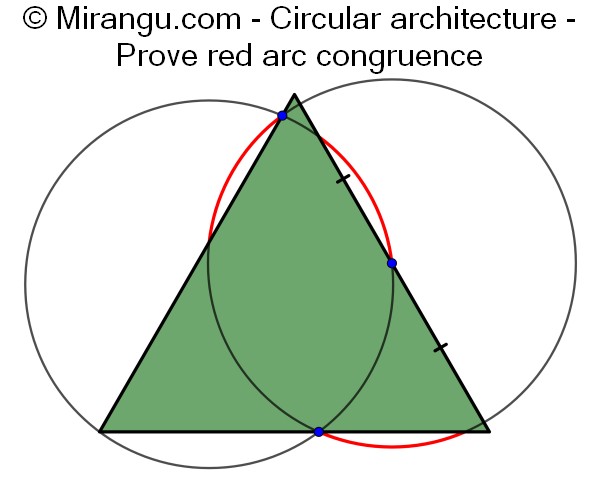
An equilateral triangle and two circles. The centre of the right circle is the triangle side midpoint. Both circle intersections lie on a triangle side. Prove that the three red circular arcs are congruent.
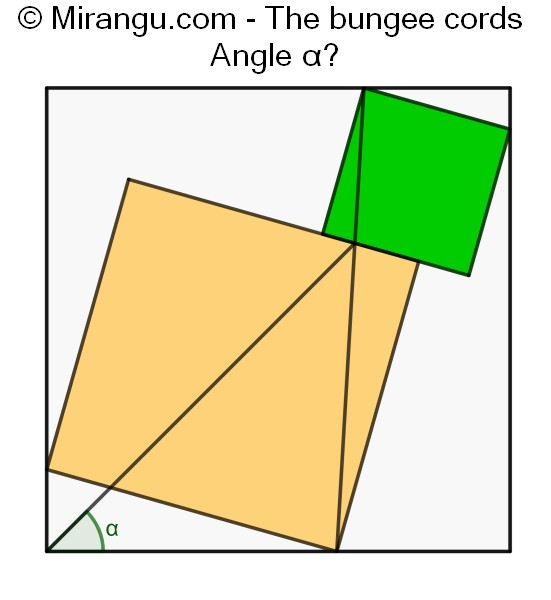
Three squares and two line segments. What’s the angle α?

Divide a rectangular piece of paper in five pieces of equal area. You only have a pair of scissors at your disposal, but you are allowed to make straight folds to guide you.
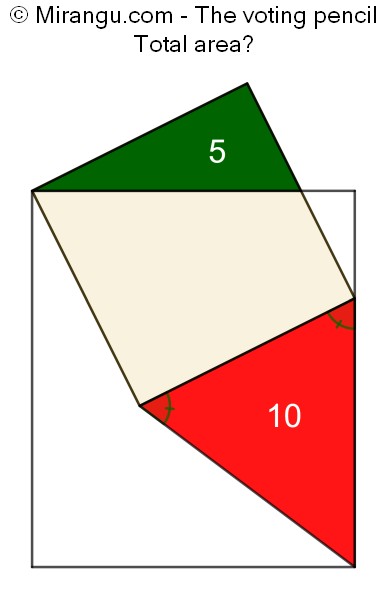
A square and a rectangle share a vertex. Two triangle areas are given. What is the total area?
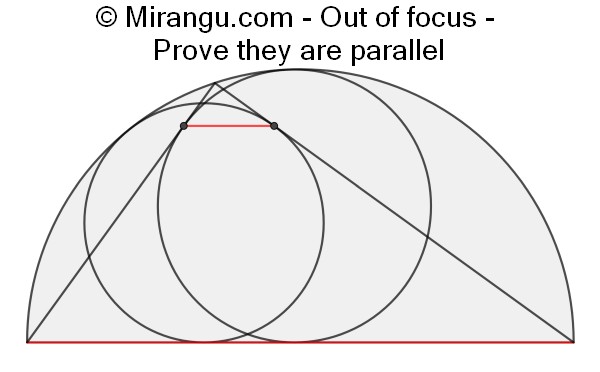
A semicircle with an inscribed triangle. Both circles are tangent to the semicircle, the diameter and one other triangle side. Prove that the line segment connecting the two shown tangency points is parallel to the diameter.
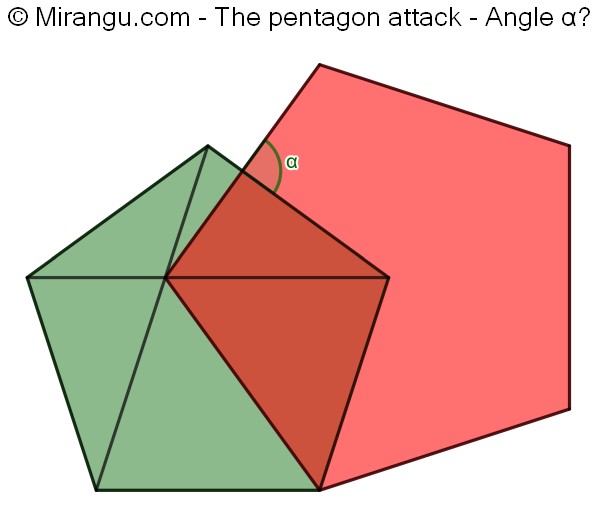
Two regular pentagons and two diagonals. What’s the angle α?
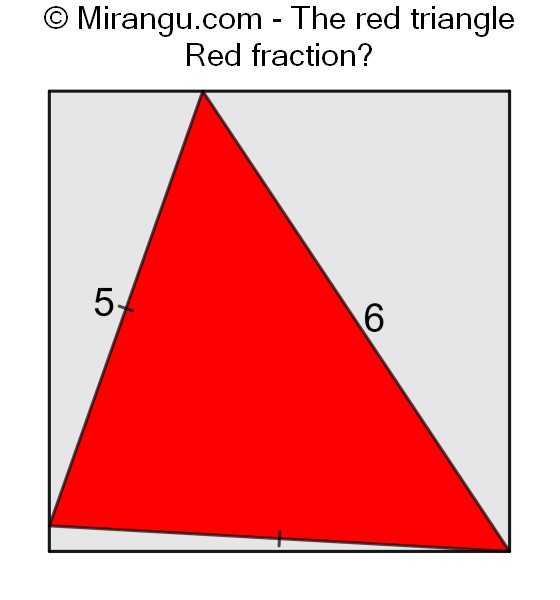
A square containing an isosceles triangle with given side lengths. What fraction is red?