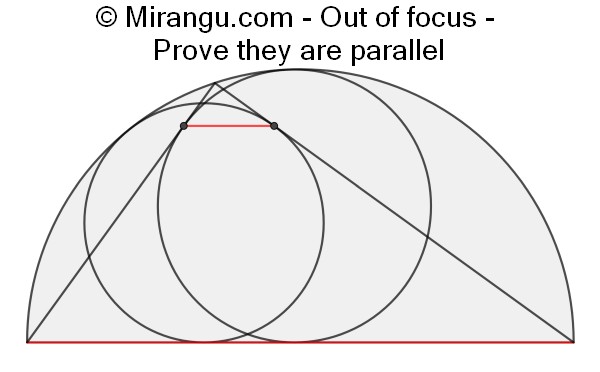
A semicircle with an inscribed triangle. Both circles are tangent to the semicircle, the diameter and one other triangle side. Prove that the line segment connecting the two shown tangency points is parallel to the diameter.
Scroll down for a solution to this problem.
Solution

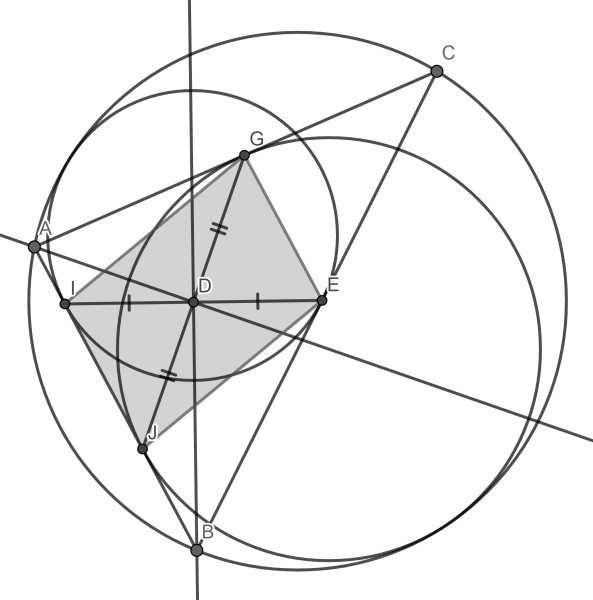
This problem can be generalised to all inscribed triangles, not just right ones. I thank Ahmet ÇETİN for pointing this out. As shown in the diagram below, one can easily proof that the four tangency points form a parallelogram by using Sawayama’s Lemma.
Poem
Out of focus
” I saw a glittering moon
I saw a beautifull morning
Shining on the hill
And I grabbed the cat by the tail
The future with my finger nails
But now I live in fear
It’s all out of focus
It’s all baby so unclear…..”

(Out of focus, Mick Jagger)