A semicircle containing two circles and two triangles. The blue right triangle connects three tangency points. Prove it is isosceles.
Sisyphus
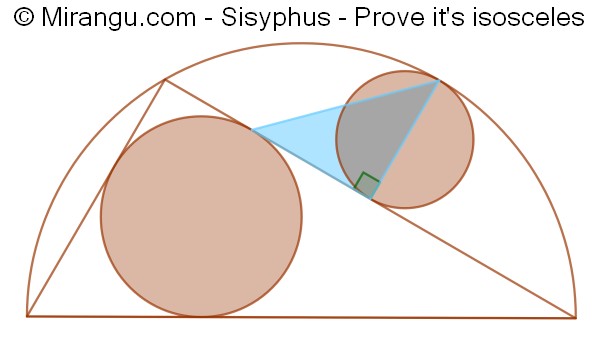

A semicircle containing two circles and two triangles. The blue right triangle connects three tangency points. Prove it is isosceles.
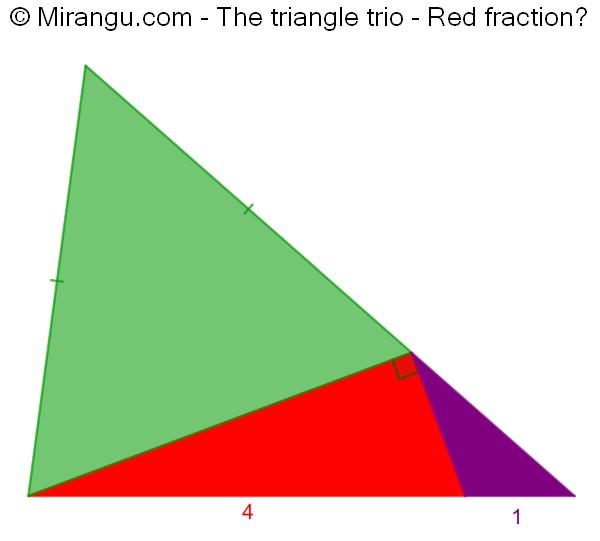
Three triangles, one of which is right and one is isosceles, form a large triangle. Two side lengths are given. What fraction of the total area is red?
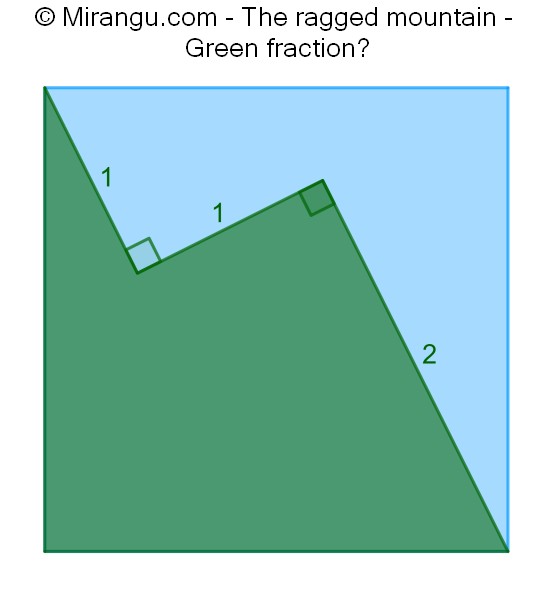
A square containing three line segments of given length. What fraction is green?
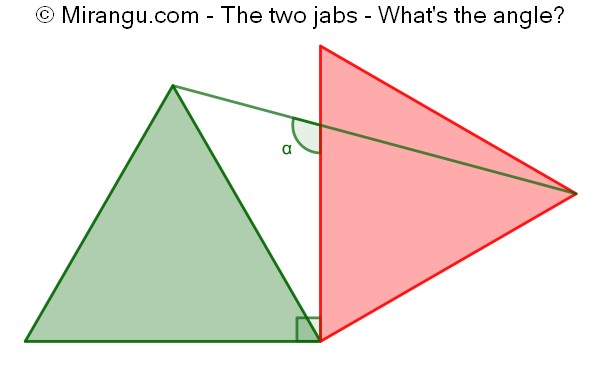
Two congruent equilateral triangles share a vertex. What is the angle α?
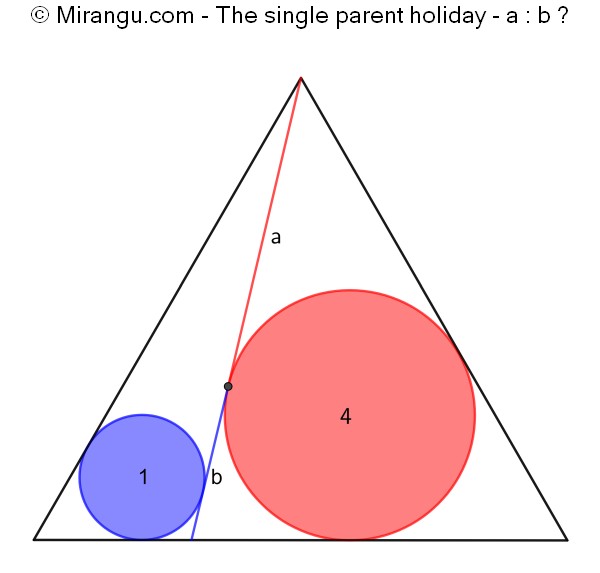
An equilateral triangle containing two circles of given area and a common tangent divided in two. What is the proportion of the two parts?
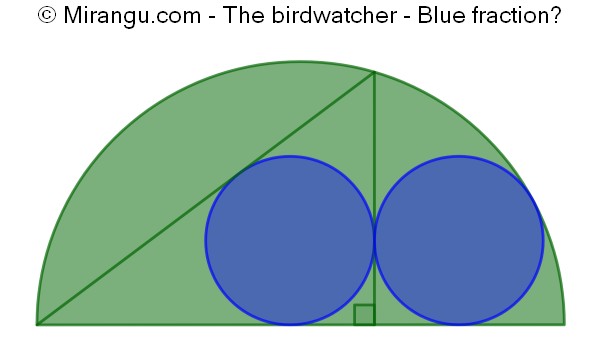
Two congruent circles and a right triangle inside a semicircle. What fraction is blue?
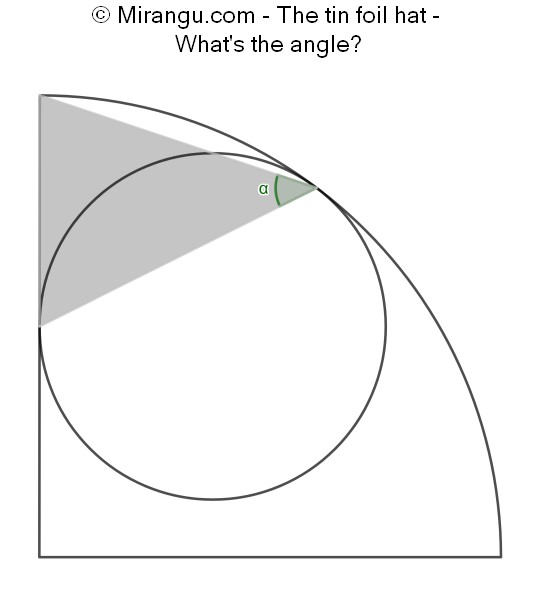
A circle inside a quarter circle. The triangle connects the two tangency points and the top of the quarter circle. What’s the angle α?
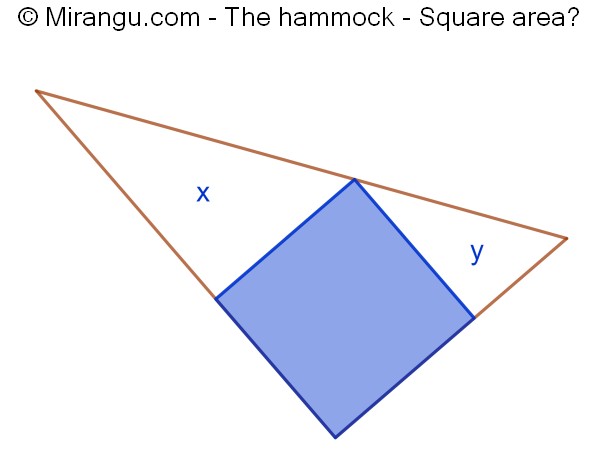
A square inscribed in a triangle. Two areas are given. What is the square’s area?
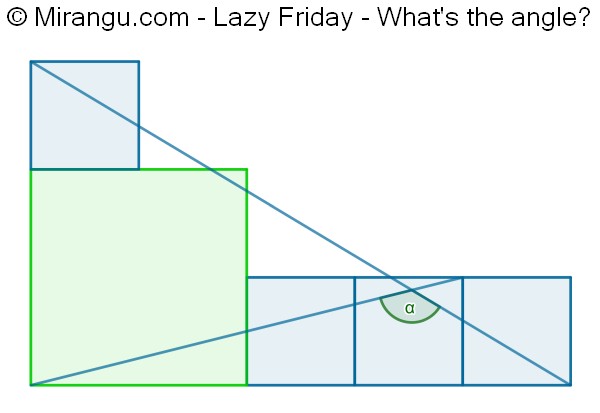
Four congruent squares plus another one. What is the angle α?
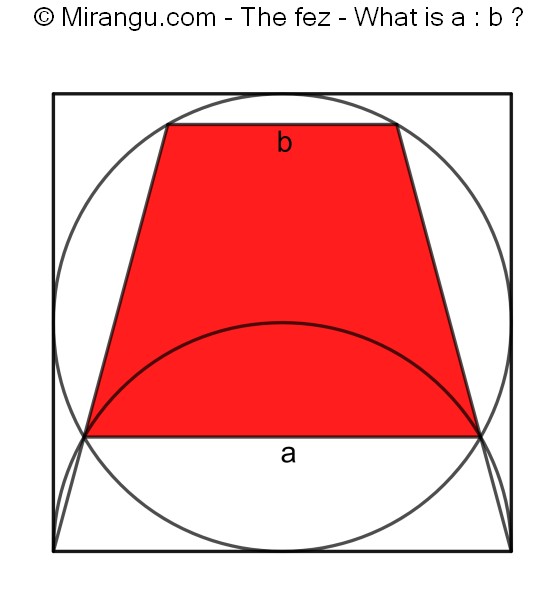
A circle and a semicircle inside a square. What’s the length proportion of the two chords?
Improve your mental health with our new book “Vitamin G, 100 wholesome geometry puzzles”.
Order now