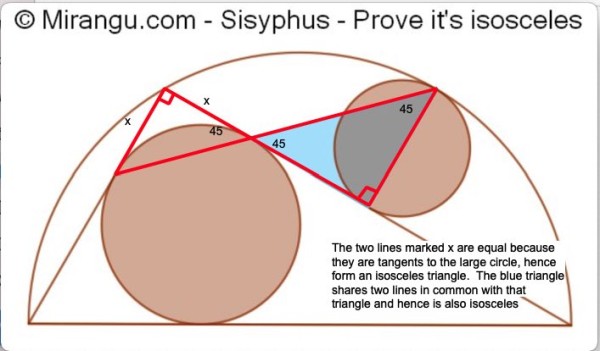
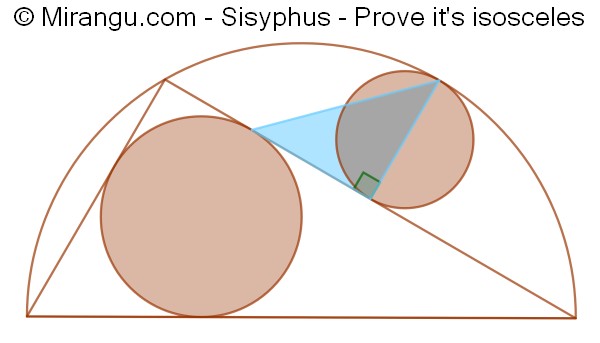
A semicircle containing two circles and two triangles. The blue right triangle connects three tangency points. Prove it is isosceles.
Scroll down for a solution to this problem.
Solution
Poem
The myth of Sisyphus
This legendary sisyphus
Obliged to roll his stone
With courage and dignity
On the mountain top
A mythical ascent
Rolling his stone painfully
Such was his destiny
Never a victory
Like a night of Gethsemani
For all it’s life
A never ending tragedy
One reply on “Sisyphus”
I think you need to specify somehow that the smallest circle is at the midpoint of the side of the larger triangle to which it is tangent.