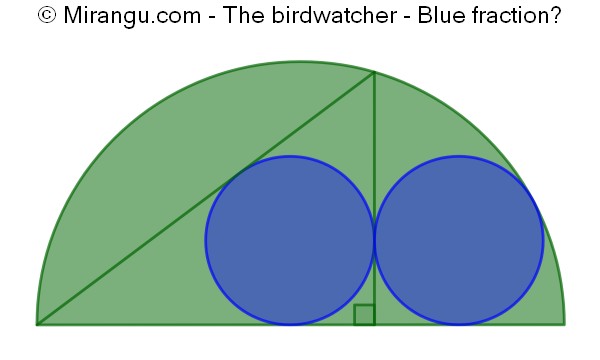
Two congruent circles and a right triangle inside a semicircle. What fraction is blue?
Scroll down for a solution to this problem.
Solution
The blue fraction is 256/625.
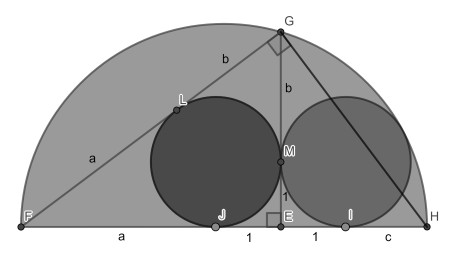
We set the radius of the two circles to 1. We can use the Pythagorean theorem in the right triangle to find that a+b-ab+1=0. Next, we use the fact that the triangle FIG is isosceles. A proof of this interesting lemma is given below.
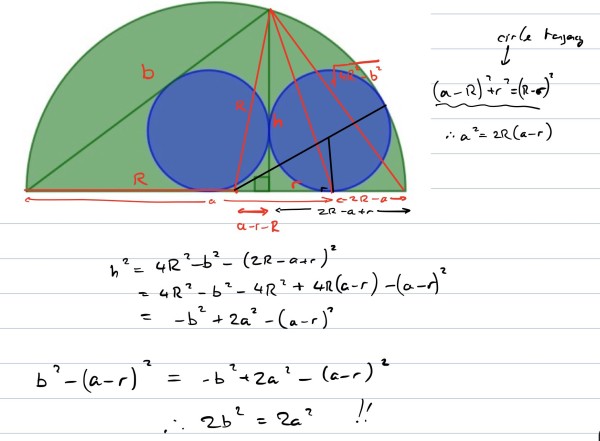
This gives us a+b=a+2, so b=2. From the previous equation it follows that a=3, so the right triangle is a 3-4-5 triangle.
Using similarity of the two smaller triangles easily gives c=5/4. The radius of the semicircle r=a/2+c/2+1=25/8. The requested fraction follows.
Poems
The birdwatcher
Knows many thrilling sights
He hunts pictures patiently
As I do for words in poetry
A poet and protector naturally
Just peace to work,
No hurry
Waiting patiently
He wins ultimately
Loving birds and words
Is a world full of mystery.