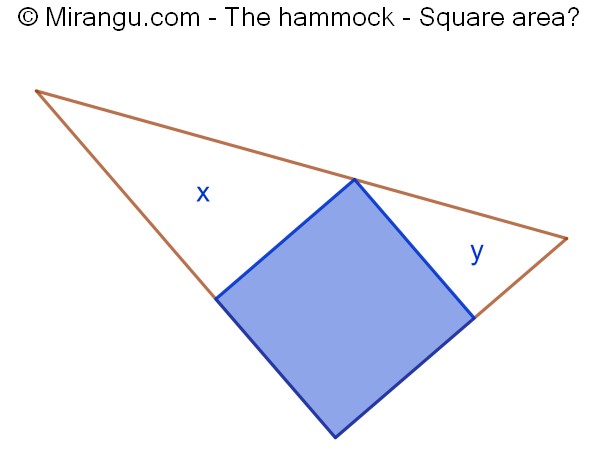
A square inscribed in a triangle. Two areas are given. What is the square’s area?
Scroll down for a solution to this problem.
Solution
The square area is 2√xy.
This problem can be solved in an algebraic way, as was shown by Dr Rick. The diagram contains three similar triangles: the unshaded ones and the big one. Their hypotenuses have proportions √x : √y : √x+√y. Their areas have proportions as the squares of that and since (√x+√y)2=x+y+2√x√y, the square must have area 2√xy.
Note that this proof also holds in case the square would be parallelogram.
Poem
The hammock
Keeps our dreams
Keeps our thoughts
From morning
To evening
We lay softly dreaming
Eyes closed, and shivering
Our hands sliding
Our bodies slowly travelling
A bird is kindly singing
A moment of eternity
Far from reality
The hammock is friendly

One reply on “The hammock”
2 (xy)^.5