Three squares. The top line segment is variable in length. What’s the minimal blue fraction?
Scroll down for a solution to this problem.
Solution
The minimal blue fraction is 1/5.
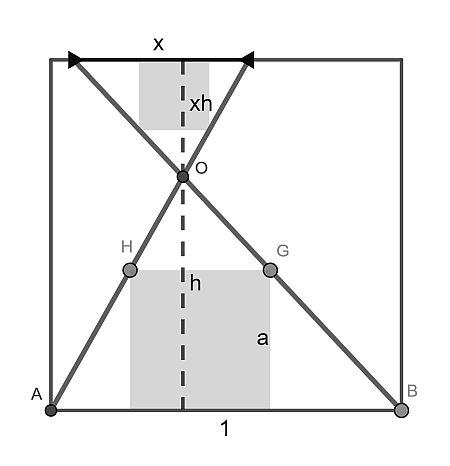
For convenience we set the square side to 1. From similarity of the two triangles formed by the oblique lines, we can calculate the lower square area and multiply by x2 to obtain the upper area. Also, we see that the sum of the heights must be 1, so h=1/(1+x).
From similarity of triangles ABO and HGO, we deduce h/1=(h-a)/a, leading to a=h/(1+h)=1/(2+x). So for the blue fraction we get A(x)=(1+x2)/(2+x)2.
To find the minimum of this function we take the derivative and set it to 0. This gives us x=1/2, corresponding to a fraction of 1/5, and this is indeed a minimum on the range [0,1].
Poem
3 squares
Red, yellow and blue
What can they do?
What is their meaning?
Just staying here in this figure
A draft for a flag?
The red colour for blood
From our soldiers
Blue for truth wisdom
A symbol for a city, a country
A flag with pride
Nobody will hide


2 replies on “Who’s afraid of red, yellow and blue?”
Interesting problem! After reading your solution, at least I understood how it is done. The challenge in problems like this is always to reduce the variable parameters to one, in order to get the derivative, and I think, it requires a lot of practice (which I never had) to “see” the path.
Thanks. You’re right about the strategy, although I think with multiple variables extremes can also be found. In any case, it involves differential calculus.