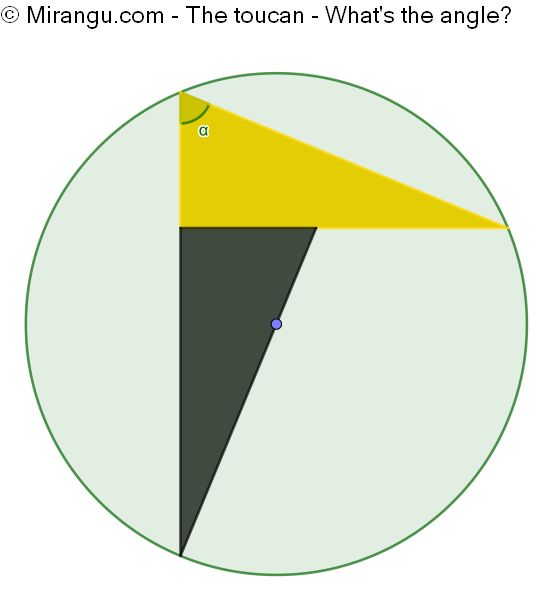
Two congruent right triangles inscribed in a circle. The circle centre lies on one of the hypotenuses. What’s the angle?
Scroll down for a solution to this problem.
Solution
The angle α is 67,5°.
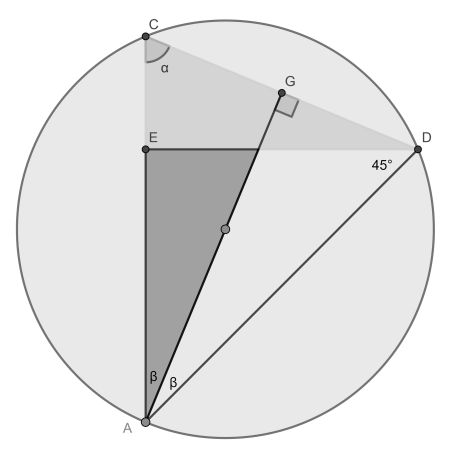
Our solution follows these steps:
- Extend the hypotenuse through the centre to point G. Using the fact that β=90-α, it makes a right angle with CD.
- Using reflection symmetry in the line through AG, triangle ADC is seen to be isosceles with a top angle of 2β.
- Triangle ADE is also isosceles because of the congruency of AE and ED. It has a top angle of 90, so both other angles are 45.
- This gives 2β=45=180-2α, resulting in α=67,5.
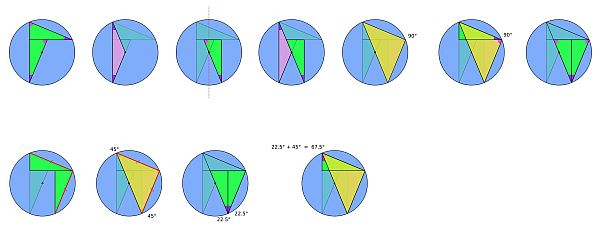
Visual solution
Poem
The coloured toucan
Who knows a toucan?
May be you can
I’ll write about that bird I can
But don’t know so much
About toucan !
So it’s more important than
Just write about two toucans
I’m his real good fan
Living in the city of Lausanne
Where I have a plan
Write about a toucan