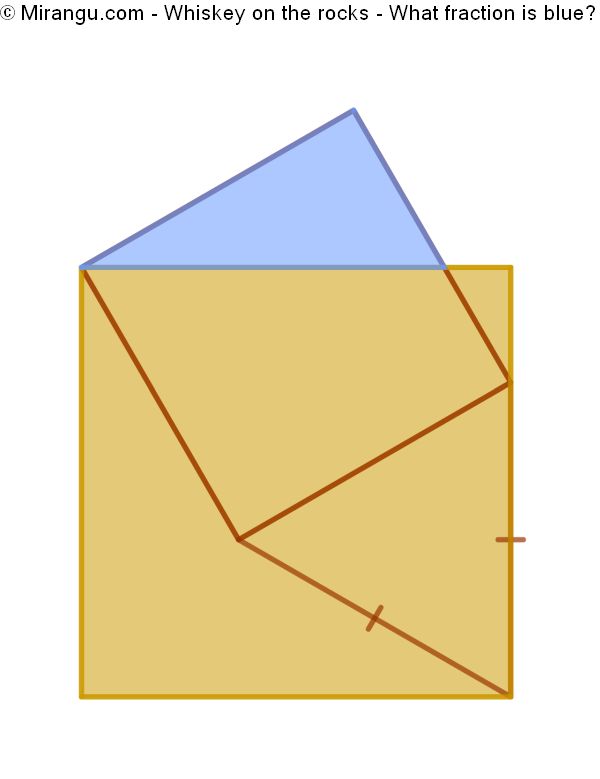
Two squares share a vertex. An isosceles triangle connects three others. What fraction is blue?
Scroll down for a solution to this problem.
Solution
The blue fraction is 1-√3/2, which is approximately 0,13.
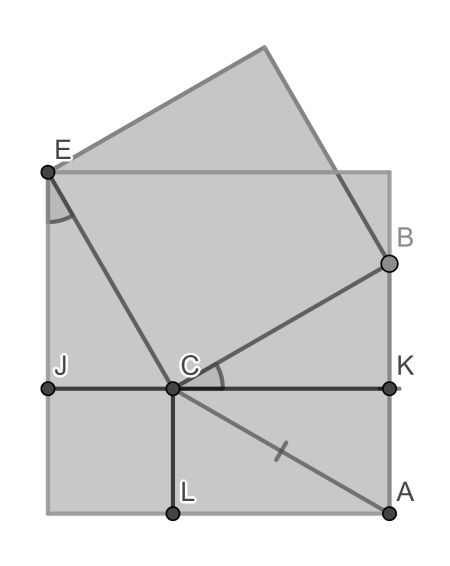
The first part of the solution is to proof that the isosceles triangle ABC is in fact an equilateral triangle. This involves the following steps:
- Triangles KBC and JCE are congruent because of AAS.
- JC is congruent with LC, because of the larger square.
- Triangles KAC and KBC are congruent because of SAS.
- All sides of triangle ABC are congruent.
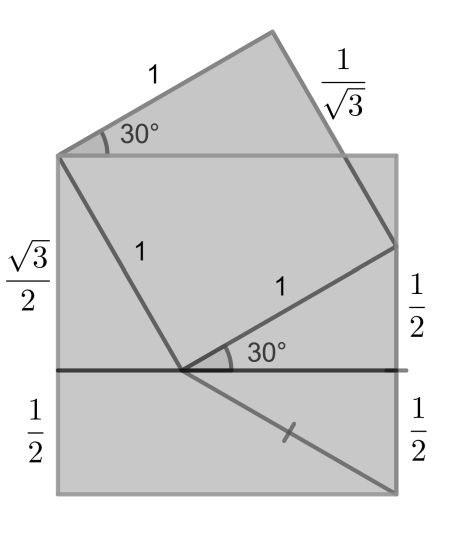
Using the above, we can easily fill in the lengths as shown, where for convenience we have taken the small square to be a unit square. The blue area is √3/6, whereas the large non-blue square measures (1/2+√3/2)2=1+√3/2. The required fraction follows.
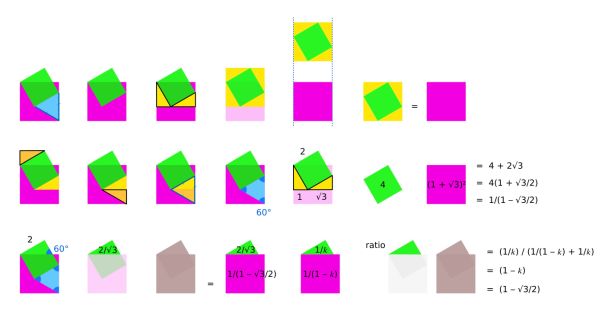
Visual solution
Poem
Just a whisky on the rocks
Whisky is not only a simple word
It’s gaelic roots means water
Whisky remembers distillation
And moments with elation
Some scottish alcoholization
Meeting in a glass liquid amber, and icy rocks for salvation
It’s the nicest drink for celebrations