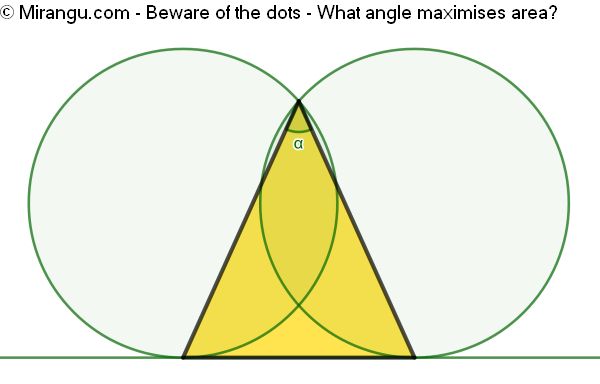
Two congruent circles and a common tangent. A triangle connecting tangency points and the upper intersection point. What angle α maximises its area?
Scroll down for a solution to this problem.
Solution
The triangle area is maximal if α is 60°.
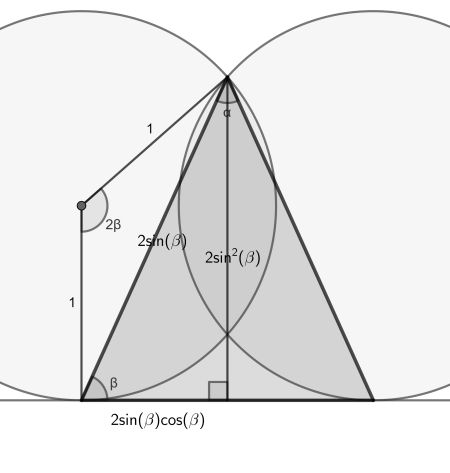
First, set the radii of the circles to 1 for convenience. Now we consider one of the lower angles β and use the fact that a circle tangent is perpendicular to the corresponding radius. We find 2β in the centre.
Therefore the triangle side is easily found to be 2sin(β). This leads to a triangle base of 4sin(β)cos(β) and a height of 2sin2(β). The triangle area is A(β)=4sin3(β)cos(β).
Now take the derivative of this function: A'(β)=4sin2(β)(3cos2(β)-sin2(β)). Setting this to zero to find extrema gives either sin2(β)=0 or tan2(β)=3. Since β lies between 45° and 90°, we find β=60°, which is indeed a maximum. Using the fact that the triangle is isosceles, it gives α=60°.
Poem
The dots are just some points
Which only help us to join
Just a position taking its place
The Greeks knew already the truth
All figures are made of points so smooth
There are many points connected
As we are to one another
Speaking to our sister or brother