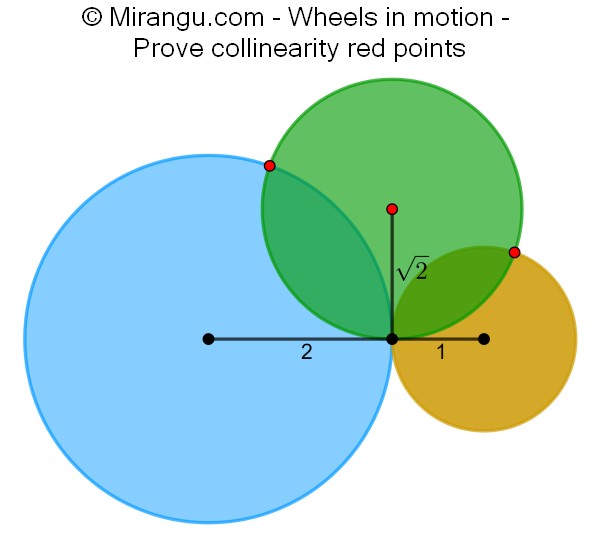
Two tangent circles and a third circle touching the line segment connecting their centres in the tangency point. Prove that the red points (centre and two intersection points) are collinear.
Scroll down for a solution to this problem.
Solution
Visual solution
Poem
Wheels in motion
Could be bicycles or car wheels
But also starting an action
Opening new perspectives and negociations
And set agreements to get the wheels in motion
I need courage
Vision and passion
To get the wheels of change in motion in time
Through this life of mine

One reply on “Wheels in motion”
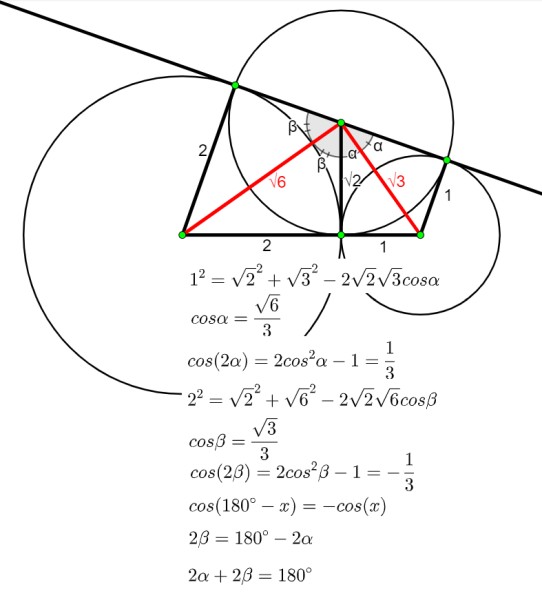
In the Soiridonov diagram the triangle with the two red sides is a right triangle, so alpha+beta=90• so the angle at middle green dot, which is 2 alpha plus 2 beta, is 180•
Thus the problem still works when the lengths 1,2,sqrt(2) are replaced by any a,b,sqrt(ab).