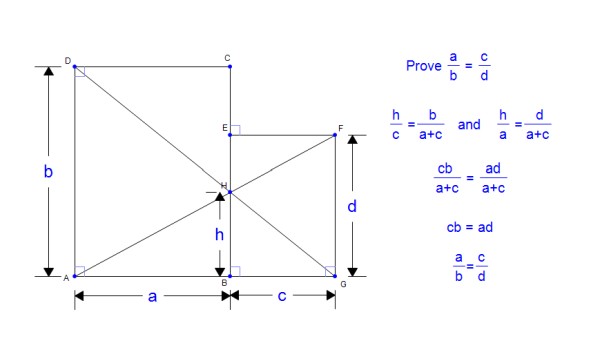
Two rectangles share a vertex. Two line segments connecting opposing vertices and the common side intersect in a single point. Prove that the rectangles are similar.
Scroll down for a solution to this problem.
Solution
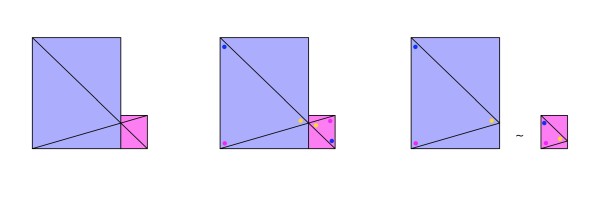
Visual solution
Poem
The miniature version
I’m smaller
Than this one much bigger
I’m a square in miniature
As important for the future
Than the blue one here
Nearly my brother
He is my lover
The blue square is larger
But I’m red and much stronger
For you our users
We are both believers

One reply on “The miniature version”
With reference to your solution diagram,
Triangles DHA and GHF are similar, giving,
HA/HF = b/d…..(1).
Triangles AHB and FHE are similar giving,
AH/FH = a/c….(2)
From (1) and (2)
b/d = a/c or a/b = c/d.