Two squares share a vertex. What fraction of the area is the overlap region?
Scroll down for a solution to this problem.
Solution
The overlap fraction is 11/25.
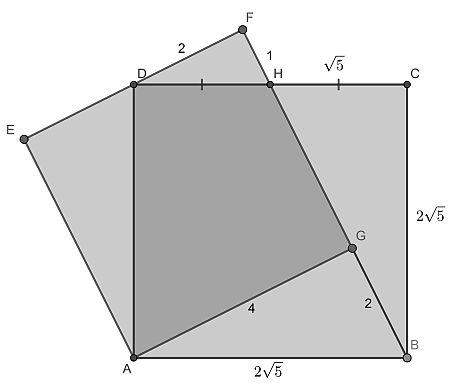
The solution starts by drawing line segment BG. By using rotational symmetry and the SAS postulate, we deduce that triangles ABG and ADE are congruent. Also, triangles ABG, ADE, DHF and BHC are similar.
Now from triangle BHC it is seen that the right-angles sides have proportion 1 : 2. Setting the small square side to 4 and using the Pythagorean theorem, we can deduce the lengths as shown above.
Now it is a matter of calculating all non-overlap areas. They add up to 1+4+4+5=14. Since the small square has area 16 and the large one 20, the overlap is calculated as (16+20-14)/2=11. The required fraction is 11/(11+14)=11/25.