A semicircle with a radius, a chord and an altitude. What is the angle?
Scroll down for a solution to this problem.
Solution
The angle α can be anything between 0° and 90°.
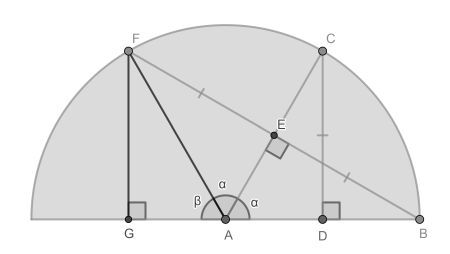
First, let me admit that I thought the answer would be 60°. This, however, is not a unique solution. Let’s see where I went wrong.
First, triangles ADC and AEB are congruent because of AAS: they share α and a right angle. Because of reflection symmetry in the radius, triangles AEB and AEF are congruent.
The last step would be to show that AEF and AGF are congruent, in which case β would equal α and 3α would equal 180°. This last step however is not allowed in general, since GF is not congruent with EF.
Ignacio Larrosa Cañestro has made an animation showing the continuum of solutions clearly.
Poem
Looking a point in the sky
The astronom counts the stars
Talking to the moon
And the planets with his heart
Day is going, night is coming
Heaven is open
Giving it’s beauty
A work of diamonds in progress
Tangling planets
Spatial dance
The sun is sleeping

One reply on “The observatory dome”
Figures are sometimes misleading, one must be very careful. But we must not fall into the Bourbaki’s hyperreaction of completely banishing them from mathematics …