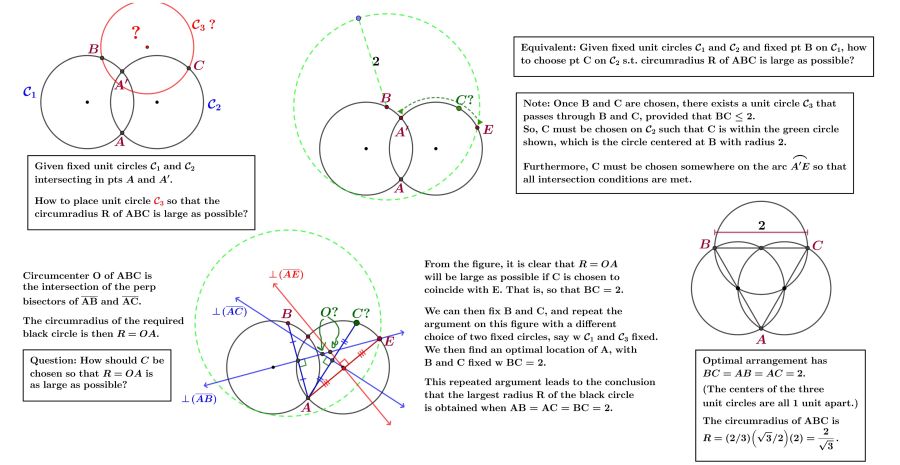
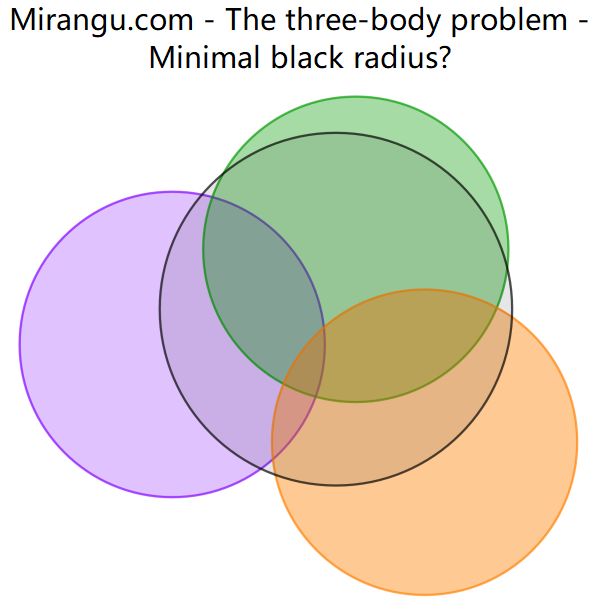
Three coloured unit disks are placed so that they have a common (3-way) intersection, but none of the disks covers the intersection of the other two disks. What is the minimum radius of the disk that would cover all intersections at once, in all cases?
Scroll down for a solution to this problem.
Solution
The minimal black radius is 2/√3.
A proof by Marshall W. Buck using inversion can be found here.
2 replies on “The three-body problem”
Here is a simple argument for why the three vertices at the ends of the 2-way intersections (the “petal tips”) fit within a circle of radius at most 2/sqrt(3).
Proposition. The three petal tips are contained in a circle of radius at most 2/sqrt(3).
The petal tips form a triangle with sides at most 2, because each is a unit distance from two of the colored disk centers. Name the side lengths of the “petal triangle” a, b, c, with opposite angles A, B, C. If the triangle is acute then there is one angle, say A, which is in the range 60 to 90 degrees.
Then, using the extended law of sines, we see that the circumcircle has a radius equal to a/(2 sin A) which is less than or equal to 2/sqrt3 because a = sqrt(3)/2. Otherwise, the petal triangle is obtuse, and there is an angle > 90 degrees. In that case, the triangle fits in a semicircle of radius at most 1 on the base opposite that angle. (The actual circumcircle through the petal tip vertices could be larger though. )
Some text seems to be have deleted before posting. Sorry about that.
It should have said a/(2 sin A) which is less than or equal to 2/sqrt(3) beccuase a is less than or equal to 2 and sin A is greater than or equal to sqrt(3)/2.
The original text used less than signs and equal signs, so maybe that got interpreted as HTML.