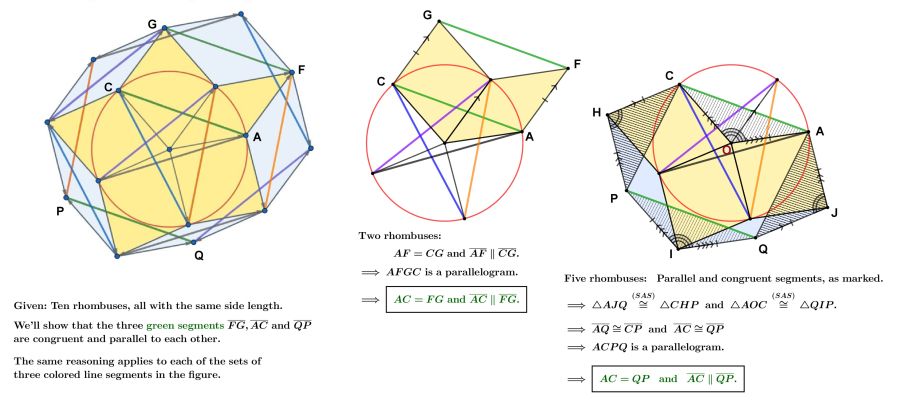
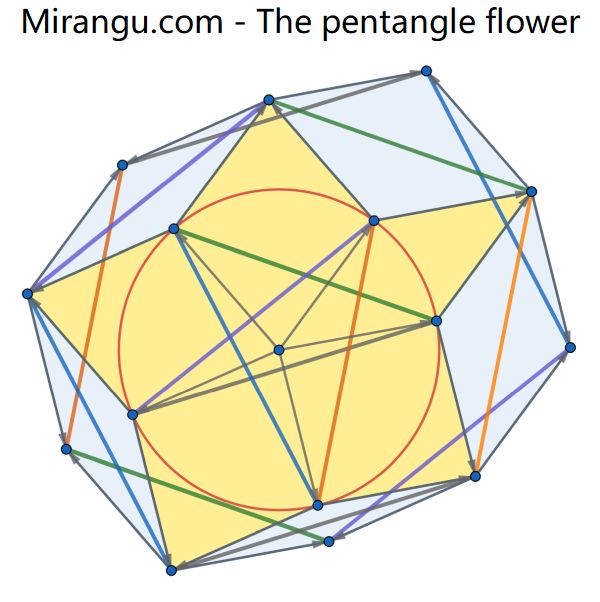
Multicoloured pentangle in a red circle. Rhombuses form two levels of petals growing outward, forming a decagon. Show that the opposite sides of the two interleaved pentagons are equal in pairs and also equal and parallel to the sides of the pentangle.
Scroll down for a solution to this problem.
Multicoloured pentangle in a red circle. Rhombuses form two levels of petals growing outward, forming a decagon. Show that the opposite sides of the two interleaved pentagons are equal in pairs and also equal and parallel to the sides of the pentangle. By @MarshallWBuck pic.twitter.com/wsOJuLKTT6
— Mirangu (@Mirangu1) August 10, 2023
One reply on “The pentangle flower”
A proof via vectors is perhaps the clearest.
If the tips of the pentangle are vectors a,b,c,d,e (from the center),
then the tips of the first round of rhombuses are a+b, b+c, c+d, d+e, e+a, and the tips of the second round are a+b+c, b+c+d, c+d+e, d+e+a, e+a+b. Differences of adjacent vectors on either list will be one of a-c, b-d, c-e, d-a, e-b (or their negatives). These 2-apart differences also represent the sides of the pentangle. Equal vectors convert to parallel line segments of equal length.