Three congruent rectangles on a line. Prove that the four red points are cyclic.
Scroll down for a solution to this problem.
Solution
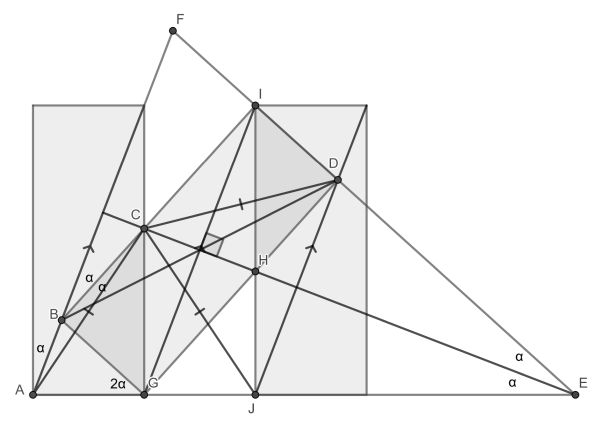
First draw three parallel diagonals, showing that the space between the standing pillars exactly fits another congruent pillar. CGHI is readily seen to be a rhombus. Also B lies in the left and D on the right diagonal. Then extend the left diagonal and the upper side of the slanted pillar to form triangle AEF. Some angle chasing easily shows it to be isosceles, the line EC being the median.
Now because ∠CBF=∠AEC we have that ABCE is cyclic. Since |AC| and |CD| both are equal to |CJ| and since ∠AEC=∠CED, we also find ACDE is cyclic. This makes ABCDE cyclic and hence also ABCD.
One reply on “Falling pillar II”
A variation