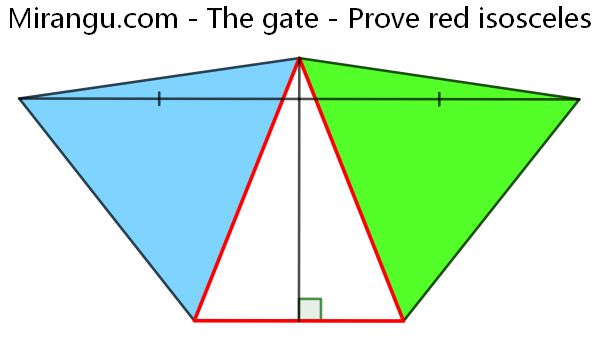
Two equilateral triangles sharing a vertex and three line segments. Prove that the red triangle is isosceles.
Scroll down for a solution to this problem.
Solution
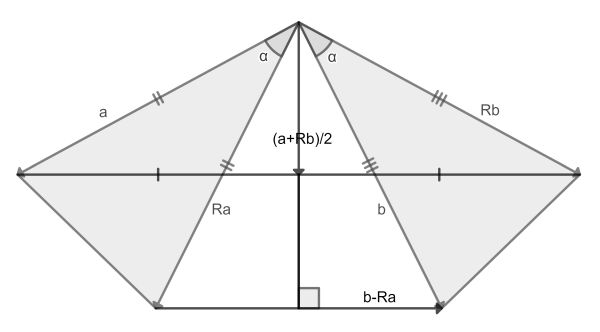
We provide a solution to the more general case of two similar isosceles triangles both having top angle α smaller than 180°. Construct vectors a and b along the sides as shown, R being a counterclockwise rotation over α. The vector connecting common vertex and midpoint is then (a+Rb)/2, whereas the bottom vertices are connected by b-Ra.
Now taking the dot product of those two, it must be 0 because of the right angle. So, (a+Rb)·(b-Ra)=0. This works out as a·b-Ra·Rb=a·Ra–b·Rb. Now the left side is 0, because rotations do not change the dot product. The right side equals (|a|2-|b|2)cos(α).
So, either α=90° which is the situation in Meeting halfway, or the triangles are congruent.
4 replies on “The gate”
If this pdf file shows up, it is another, perhaps simpler, proof of the original, ungeneralized problem.
Here I try a jpeg file as requested.
One more way for the generalisation:
A mistake in my post (I moved B1 after writing the text):
The text in the picture above was made for B1 at the left of C.
A and B in the figure are on the same side of (B1 C1) and so C is on k1 as the angle(B1, C, C1) = alpha. – Sorry