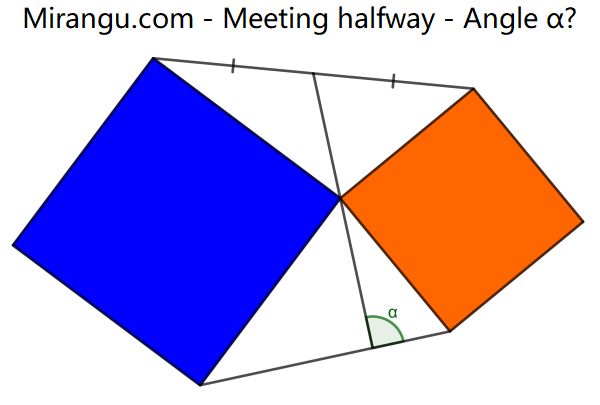
Two squares and three line segments. What’s the angle α?
Scroll down for a solution to this problem.
Solution
The angle α is 90°.
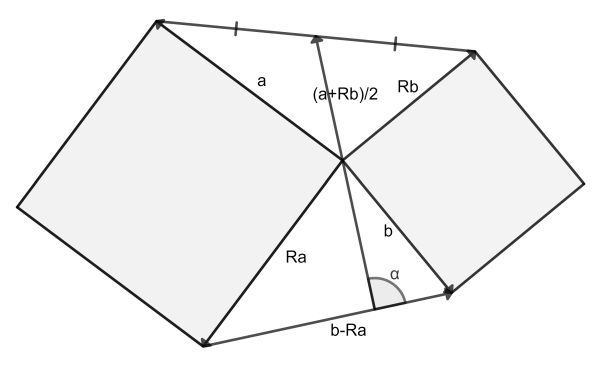
We define the vectors a and b along the respective square sides, as well as Ra and Rb, where R is an anticlockwise rotation over 90°. Now consider the vector to the midpoint: it is (a+Rb)/2. The vector connecting the lower vertices is b-Ra.
Taking their dot product we get (a+Rb)·(b-Ra)/2=(a·b-Rb·Ra–a·Ra+Rb·b)/2. Now the last two terms are 0, because these vectors are perpendicular. We also know that a rotation does not alter the (commutative) dot product, so the first two terms cancel each other. The total dot product is therefore 0, implying that α is right angle.