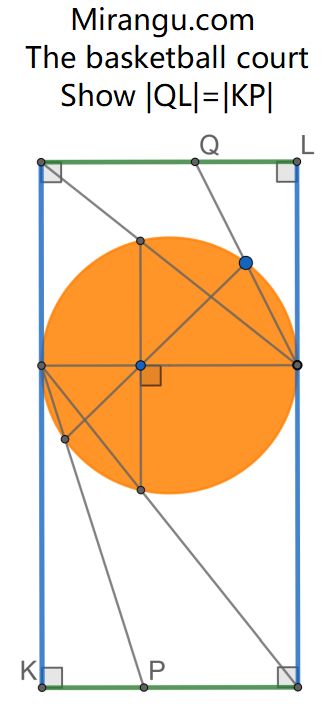
An orange circle is squeezed inside a rectangle. Show that no matter how the blue point moves on the circle, the derived points Q and P will satisfy |QL| = |KP|.

Solution

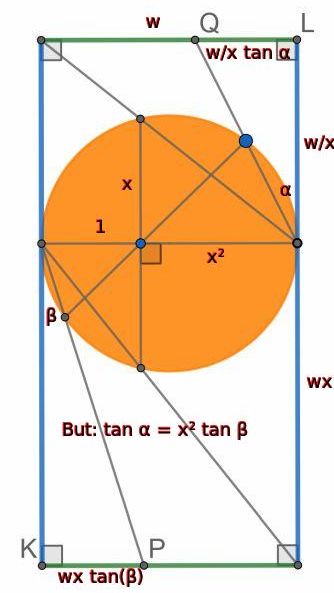
This makes use of the following lemma:

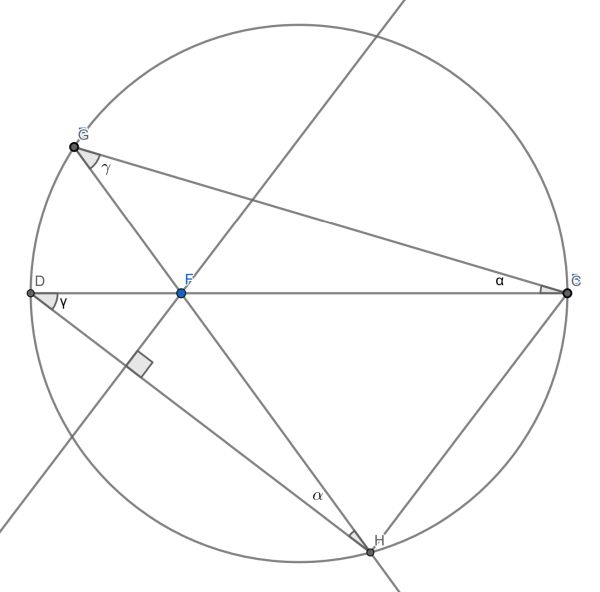
We have a circle with diameter and two chords, GC and DH, related by a fixed point F on the diameter (namely G,F,H are collinear). We need to show that tan(α) is a fixed constant times tan(γ). But, the perpendicular dropped from F to the bottom chord DH splits the chord in the same proportion that F splits the diameter DC, because that dropped perpendicular line is parallel to the chord HC (both being perpendicular to DH). Thus, tan(α)*CF = tan(γ)*DF, so the ratio tan(α)/tan(γ) = DF/CF, which is fixed because F is fixed.

An orange circle is squeezed inside a rectangle. Show that no matter how the blue point moves on the circle, the derived points Q and P will satisfy |QL| = |KP|. https://t.co/xqfWZVzvN4 By @MarshallWBuck pic.twitter.com/PeGWrscODr

— Mirangu (@Mirangu1) August 24, 2023