A square containing a red square of variable size sharing a vertex with a blue rectangle. What is the maximal blue fraction?
Scroll down for a solution to this problem.
Solution
The maximal blue fraction is 1.
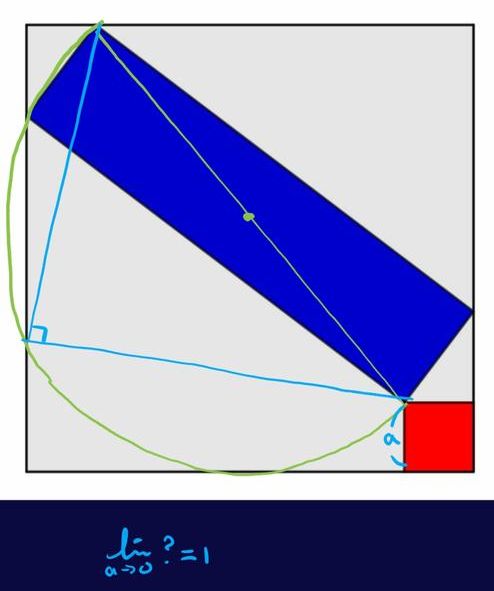

A square containing a red square of variable size sharing a vertex with a blue rectangle. What is the maximal blue fraction?
Scroll down for a solution to this problem.
The maximal blue fraction is 1.

A square containing a red square of variable size sharing a vertex with a blue rectangle. What is the maximal blue fraction? https://t.co/ct23uNJfmX pic.twitter.com/2c3LajzJIw
— Mirangu (@Mirangu1) October 5, 2022
One reply on “The maxbox”
When the orange length is 1/5 of the large square, there is only one blue rectangle. If the orange square is smaller than that, there are two solutions, and if the orange square is larger than 1/5, then there are no blue rectangles satisfying the constraint. The area of the blue rectangle is 2/5 of the full square in the unique-solution case. Perhaps someone can write out the details, if these assertions are correct.