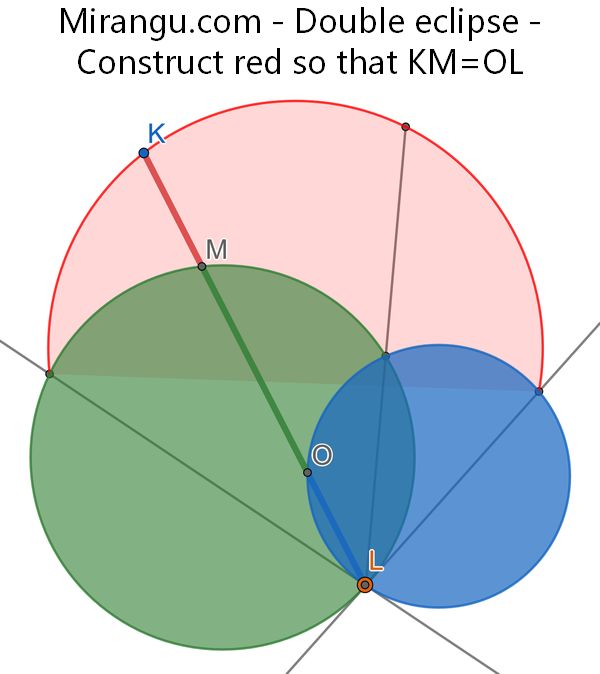
Given green and blue discs, construct a red region so that for every ray leaving L stays in the blue region exactly as long as it does in the pink region. (Namely, KM = OL.)
Scroll down for a solution to this problem.
Solution

Proof that the locus of K is a circle using two tangents in L.
2 replies on “Double eclipse”
This problem is a geometrical embodiment of the simple fact that the sum of two sine waves, with different amplitudes and time offsets, is still one sine wave. (Here the sine wave functions are the lengths of chords from a point on the circle, as a function that the chord makes to some fixed line. The chord length is the diameter length times the cosine of the angle between the chord and the diameter.)
Nice connection, so with my dot product solution, we have p.p = p.r ∴ |p|² = |p||r|cos θ ∴ |p| = |r| cos θ, a nice polar equation.