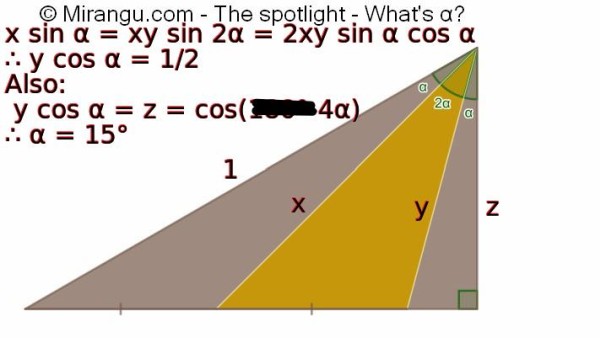
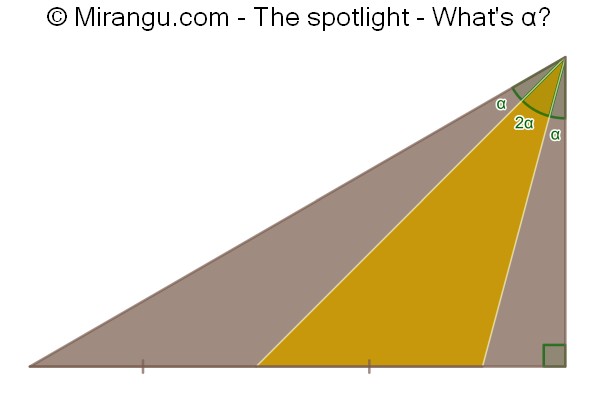
A right triangle with two cevians. What’s the angle α?
Scroll down for a solution to this problem.
Solution
The angle α is 15°.
Poem
Today we live in Covidie
Which puts the spotlight
On world’s economy
News and fake news all day
That does not help the virus to go away
A viral world, what a dismay
The virus will destroy and stay
No hugs, no hand shake
No kissing
All news by mail
And all our wishes just fail
3 replies on “The spotlight”
a=15 graden
Heel goed Marian, hoe heb je dat gevonden?
I did this the hard way. 🙂
Start with tan(4a)-tan(3a) = tan(3a)-tan(a).
Set x = tan(a), and then have
tan(4a)= (4x-4x^3)/(1-6x^2+x^4)
tan(3a) = (3x-x^3)/(1-3x^2).
Need to solve:
tan(4a)+tan(a) = 2*tan(3a),
which translates to:
(4x-4x^3)/(1-6x^2+x^4) + x == 2*(3x-x^3)/(1-3x^2).
Divide by common factor x.
Then replace x^2 by t.
Clear denominators, and get
t^3 – 13*t^2 -13*t + 1 == 0
which factors (t^2 – 14*t + 1)*(t + 1)
The root t=7-sqrt(3) gives x = 2-sqrt(3), which is the tangent of 15 degrees.