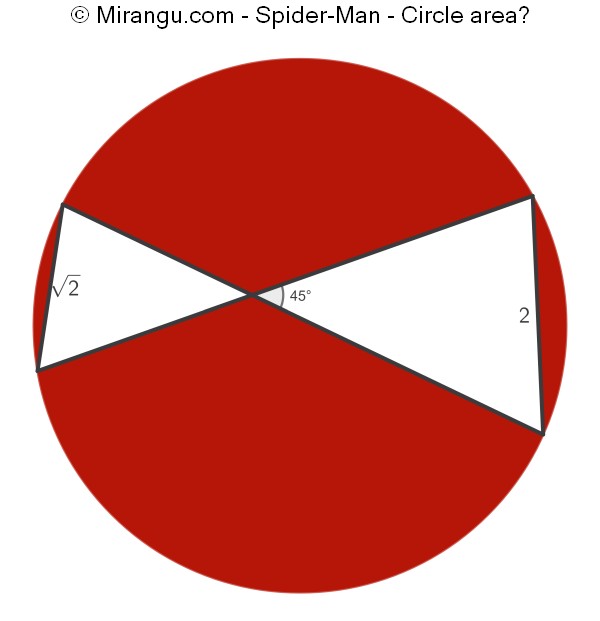
A circle with four chords. Two chord lengths are given. What is the circle area?
Scroll down for a solution to this problem.
Solution
The circle area is 5π.
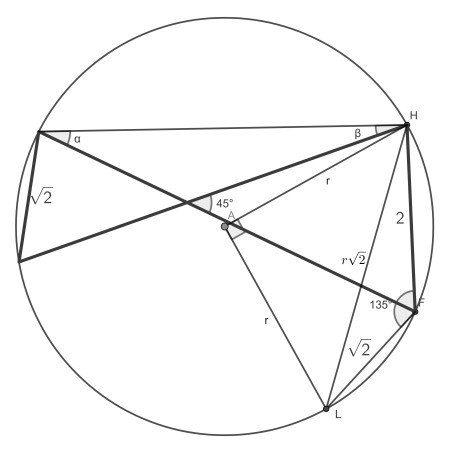
First, construct the angles α and β subtended at the circumference by the given chords. It is quite easy to see from the triangle interior angle sum that α+β=45°.
Now rotate the short chord all the way along the circle until it sits next to the longer chord. Their total angle subtended at the circumference is still 45°. Because they form a cyclic quadrilateral, the angle between the chords must be 135°.
From the Inscribed angle theorem it follows that the angle subtended at the centre is 90°. The combined chord HL therefore has length r√2. Applying the cosine rule in triangle HLF gives 2r2=4+2-√2cos(135)=10. The circle area follows.
Poem
Just a spiderman
Hanging at a thread with fun
For me, you and everyone
He is fighting crimes
On the walls he can climb
He’s a good hider
A man like a spider
He flies from there to here
To save you
He can catch the enemies
Just like flies
He wears red and blue
and he can just do