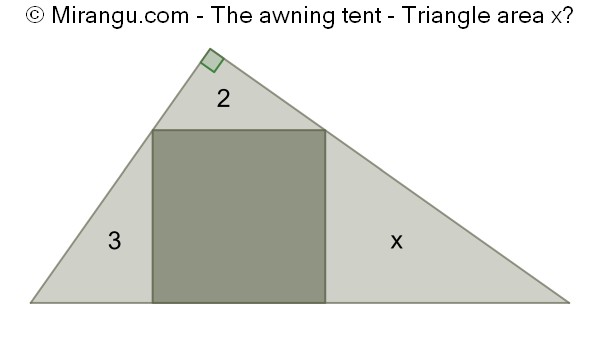
A right triangle with an inscribed square. What is the area of the triangular part on the right?
Scroll down for a solution to this problem.
Solution
The area x is 6.
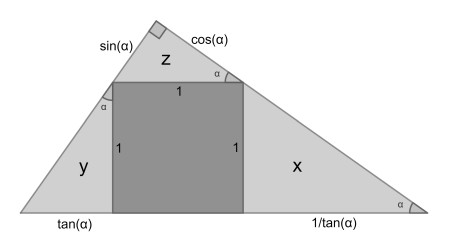
First we deduce a general theorem by Thanos Kalogerakis relating areas x, y en z. These triangles are all similar. Name the common smallest angle α and set the square side to 1. The right-angled sides can be found as shown.
Now x=1/(2tan(α)), y=tan(α)/2 and z=sin(α)cos(α)/2. Calculate 1/x+1/y=2tan(α)+2/tan(α)=2sin(α)/cos(α)+2cos(α)/sin(α)=2/(sin(α)cos(α))=1/z. So we have the equation 1/x+1/y=1/z. Using y=3 and z=2, it follows that x=6.
Visual solution
Poem
The awning tent
Stretching tightly and transparent
Used to cover thermal solar
And sometimes also in winter
Aluminium is the structure
Against cold and warm factors
Awning is like a canopy
A woven mat like a velarium
As deployed above Colosseum.
Protecting tent and aluminium