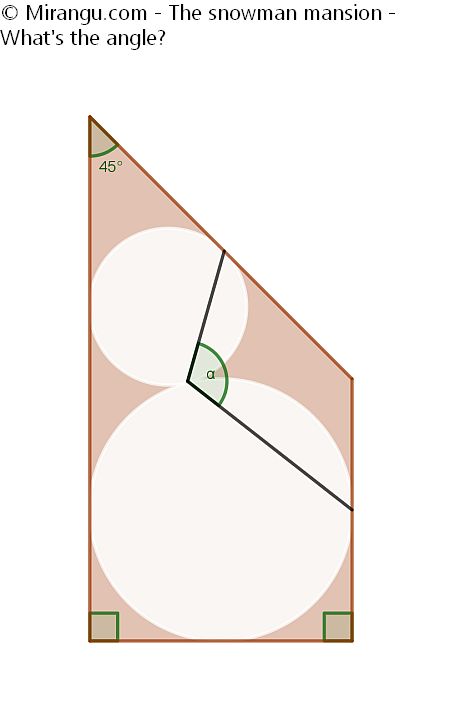
A square and a half square are stacked in order to form a house-shaped quadrilateral. Inside two circles are closely packed. What’s the angle between the tangency points?

Solution

The angle α is 112,5°.

The solution constructs the three angles at tangency point K, leading to α as the rest.

Firstly, the angle FKO can be seen to be a right angle, using the fact that OF is a diameter and the Thales theorem.

Next the angle OKM is also 90°. This can be seen if you draw the common tangent to L and compare the line segments to the other tangency points. Using the Tangent-tangent theorem, you can show that they are all equal. Hence one can draw a circle and again apply Thales.

Angle MHJ is seen to be 135°, by adding up the angles in quadrilateral MHJA. Using the Inscribed angle theorem, the final angle MKJ is seen to be 67,5°.