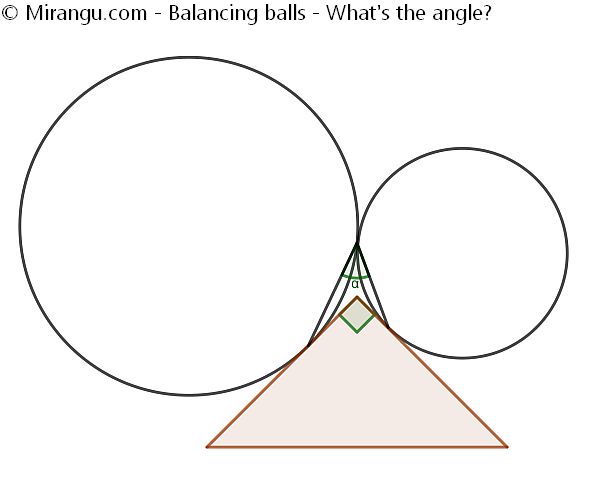
Two touching circles are placed on top of a right triangle. What’s the angle between the chords connecting the tangency points?

Solution

The angle α is 45°.

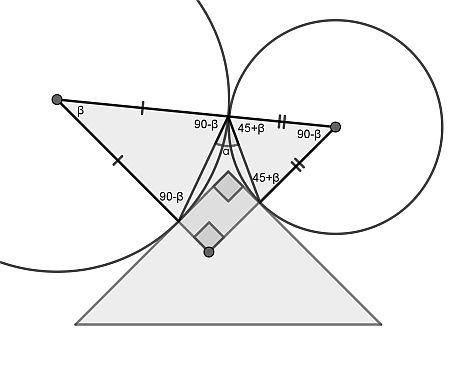
Extend the radii through the tangency points into the triangle and mark the crossing point. Now this point forms a triangle with the circle centres as shown. Using the interior angle sum, the overlapping quadrilateral is seen to be a rectangle, making the triangle a right triangle.

Now again applying the interior angle sum, the angles can be calculated as shown, using the fact that the circles enforce two isosceles triangles inside. It follows that α=45°.