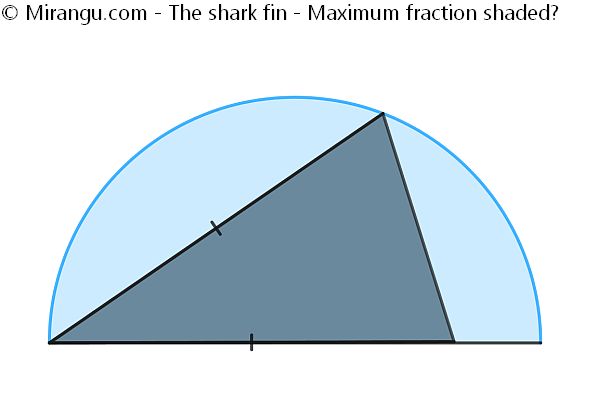
An isosceles triangle is inscribed in a semicircle with one side along the diagonal and the top vertex somewhere on the semicircle. What’s the maximum fraction shaded?
Scroll down for a solution to this problem.
Solution
The maximum fraction is (8√3)/(9π) which is approximately 0,49.
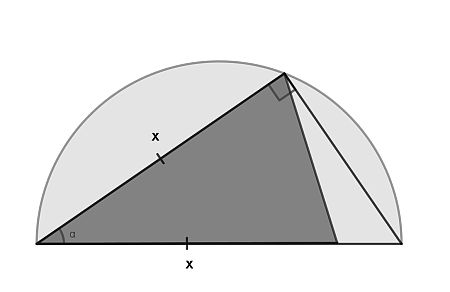
Throughout we set the radius of the semicircle to 1. Now calling the equal sides x, we use the formula that the surface of the triangle equals x2sin(α)/2. We can express x in terms of α, using the right triangle with hypotenuse 2 as shown. We get that x=2cos(α).
The triangle surface in terms of α alone is A(α)=2cos2(α)sin(α). The rest of the proof is a matter of calculus. Looking for a maximum, one takes the derivative of A(α) and sets it to 0. It is left to the reader to find that the maximum lies at cos(2α)=1/3, hence cos(α)=√(2/3) and sin(α)=√(1/3), leading to the required result. Note that is is at an angle α of approximately 35°.